Wolfram Data Repository
Immediate Computable Access to Curated Contributed Data
Social network of friendships
Social network of friendships between 34 members of a karate club at a US university in the 1970s.
(34 vertices, 78 edges)
Retrieve the graph:
| In[1]:= |
| Out[1]= | 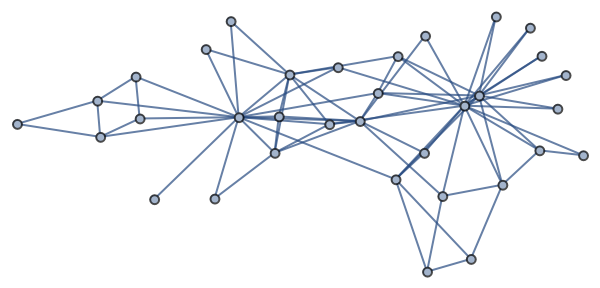 |
Summary properties:
| In[2]:= |
| Out[2]= | 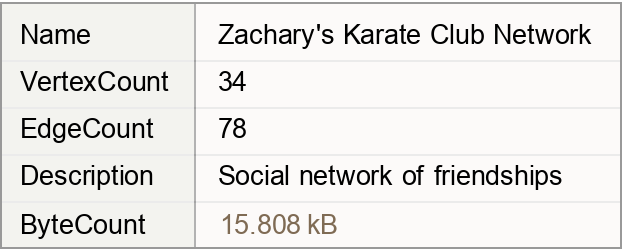 |
Find communities in the friendship network:
| In[3]:= |
| In[4]:= |
| Out[4]= |
Predict the split of the network in case of a conflict:
| In[5]:= |
| Out[5]= | 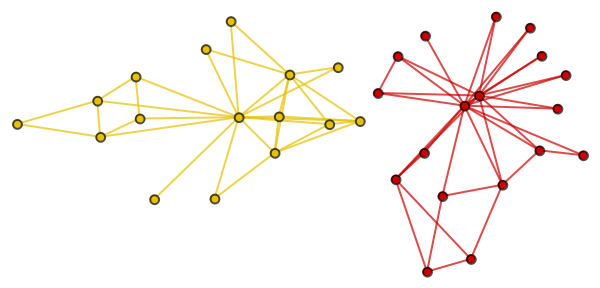 |
Wolfram Research, "Zachary's Karate Club Network" from the Wolfram Data Repository (2019)