Examples
Basic Examples (3)
Retrieve the model:
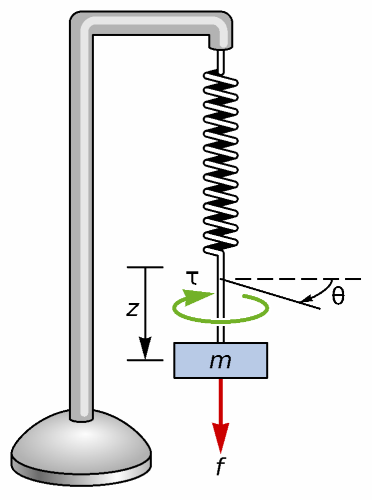
The icon:
The annotation:
Scope & Additional Elements (4)
Available content elements:
The available model types:
The operating point:
The parameters:
Visualizations (4)
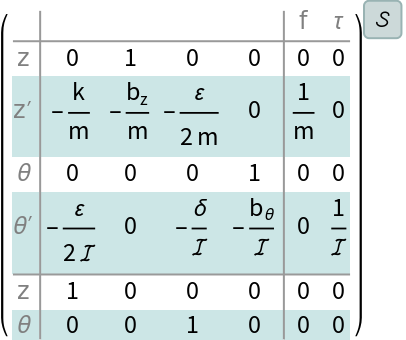
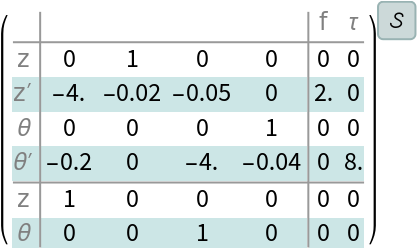
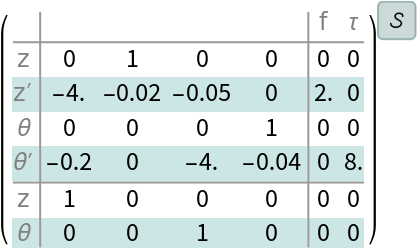
The numerical state space model:
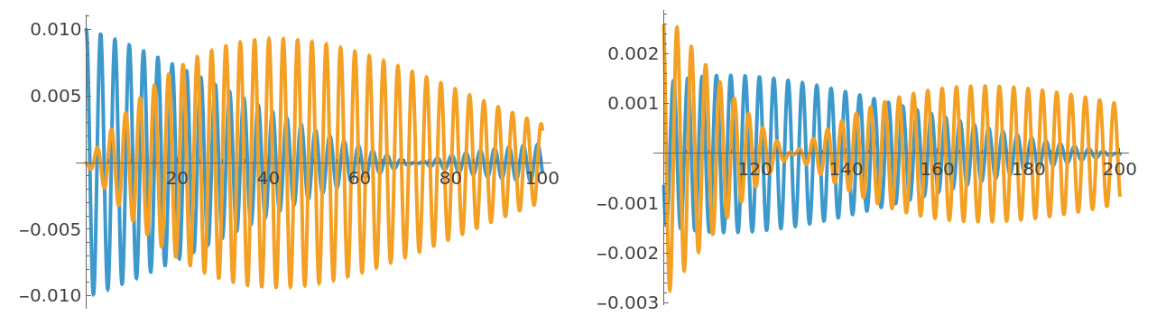
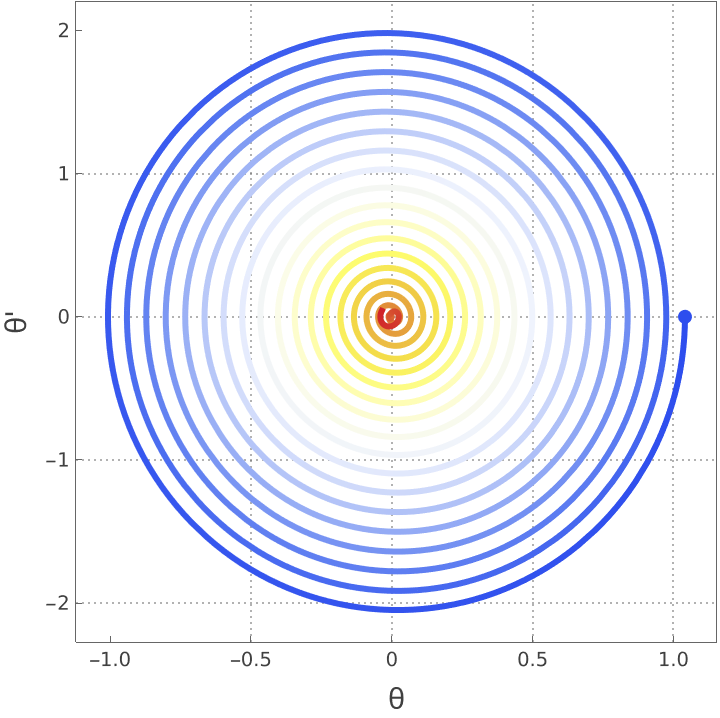
It's state response to an initial angular displacement:
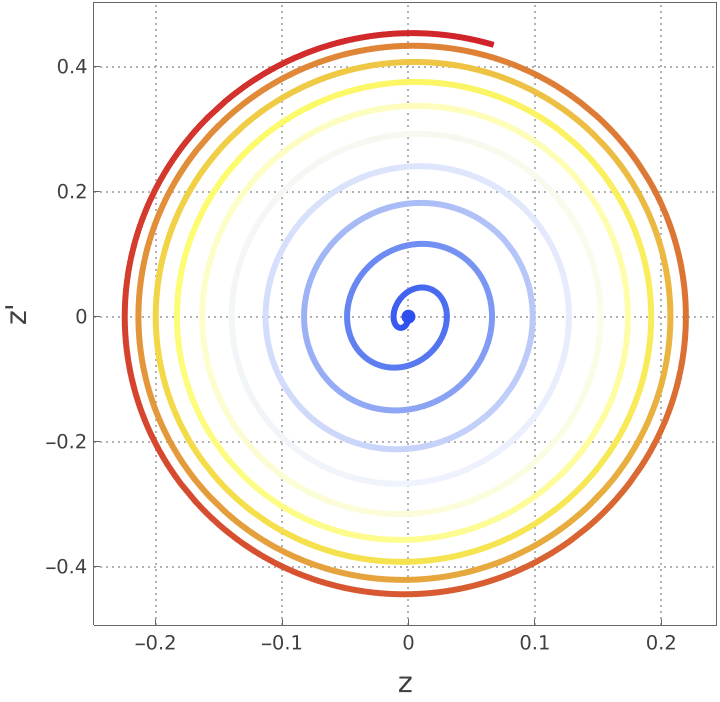
A parametric plot of the vertical position and its velocity:
A parametric plot of the angular position and its velocity:
Analysis (4)
The numerical state space model:
Compute the translational oscillation frequency:
It's the same as the rotational oscillation frequency:
This enables the beat phenomenon, transferring energy between translational and rotational motions:
Bibliographic Citation
Suba Thomas,
"Wilberforce Pendulum Model"
from the Wolfram Data Repository
(2025)
Data Resource History
Publisher Information


![ssm = ResourceData[\!\(\*
TagBox["\"\<Wilberforce Pendulum Model\>\"",
#& ,
BoxID -> "ResourceTag-Wilberforce Pendulum Model-Input",
AutoDelete->True]\)] /. ResourceData[\!\(\*
TagBox["\"\<Wilberforce Pendulum Model\>\"",
#& ,
BoxID -> "ResourceTag-Wilberforce Pendulum Model-Input",
AutoDelete->True]\), "Parameters"]](https://www.wolframcloud.com/obj/resourcesystem/images/064/0642ff3d-f644-452e-a4f7-79b1f137ced5/775884cdcfed5440.png)

![ssm = ResourceData[\!\(\*
TagBox["\"\<Wilberforce Pendulum Model\>\"",
#& ,
BoxID -> "ResourceTag-Wilberforce Pendulum Model-Input",
AutoDelete->True]\)] /. ResourceData[\!\(\*
TagBox["\"\<Wilberforce Pendulum Model\>\"",
#& ,
BoxID -> "ResourceTag-Wilberforce Pendulum Model-Input",
AutoDelete->True]\), "Parameters"]](https://www.wolframcloud.com/obj/resourcesystem/images/064/0642ff3d-f644-452e-a4f7-79b1f137ced5/6fd1eb4a19fb990e.png)
![Sqrt[k/m] /. ResourceData[\!\(\*
TagBox["\"\<Wilberforce Pendulum Model\>\"",
#& ,
BoxID -> "ResourceTag-Wilberforce Pendulum Model-Input",
AutoDelete->True]\), "Parameters"]](https://www.wolframcloud.com/obj/resourcesystem/images/064/0642ff3d-f644-452e-a4f7-79b1f137ced5/1210ac390db296ec.png)
![Sqrt[\[Delta]/\[ScriptCapitalI]] /. ResourceData[\!\(\*
TagBox["\"\<Wilberforce Pendulum Model\>\"",
#& ,
BoxID -> "ResourceTag-Wilberforce Pendulum Model-Input",
AutoDelete->True]\), "Parameters"]](https://www.wolframcloud.com/obj/resourcesystem/images/064/0642ff3d-f644-452e-a4f7-79b1f137ced5/7e04199943864cb6.png)