Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Elastic Pendulum Model

Source Notebook

Model of an elastic pendulum

Examples

Basic Examples (2) 

Retrieve the model:

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Elastic Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Elastic Pendulum Model-Input", AutoDelete->True]\)]
Out[1]=

The icon:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<Elastic Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Elastic Pendulum Model-Input", AutoDelete->True]\), "Icon"]
Out[2]=

Scope & Additional Elements (4) 

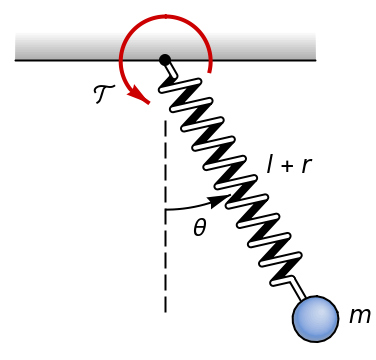Available content elements:

In[3]:=
\!\(\* TagBox[ RowBox[{"ResourceObject", "[", "\"\<Elastic Pendulum Model\>\"", "]"}], #& , BoxID -> "ResourceTag-Elastic Pendulum Model-Input", AutoDelete->True]\)["ContentElements"]
Out[3]=

The available model types:

In[4]:=
ResourceData[\!\(\* TagBox["\"\<Elastic Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Elastic Pendulum Model-Input", AutoDelete->True]\), "AvailableModelTypes"]
Out[4]=

The operating point:

In[5]:=
ResourceData[\!\(\* TagBox["\"\<Elastic Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Elastic Pendulum Model-Input", AutoDelete->True]\), "OperatingPoint"]
Out[5]=

The parameters:

In[6]:=
ResourceData[\!\(\* TagBox["\"\<Elastic Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Elastic Pendulum Model-Input", AutoDelete->True]\), "Parameters"]
Out[6]=

Analysis (3) 

The numerical model of the system:

In[7]:=
nssm = ResourceData[\!\(\* TagBox["\"\<Elastic Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Elastic Pendulum Model-Input", AutoDelete->True]\), "NonlinearStateSpaceModel"] /. ResourceData[\!\(\* TagBox["\"\<Elastic Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Elastic Pendulum Model-Input", AutoDelete->True]\), "Parameters"]
Out[7]=

Its state response starting from a horizontal position:

In[8]:=
sr = StateResponse[{nssm, {0, 0, 90 °, 0}}, 0, {t, 0, 4}]
Out[8]=

The parametric plots of the response:

In[9]:=
With[{psr = Partition[sr, 2]}, {psr, {{"r", "r'"}, {"\[Theta]", "\[Theta]'"}}, psr /. t -> 0}\[Transpose]];
In[10]:=
Grid[{Table[ ParametricPlot[a[[1]], {t, 0, 4}, Sequence[ PlotTheme -> "Web", AspectRatio -> Full, Frame -> True, FrameLabel -> Part[a, 2], Axes -> False, ColorFunction -> (ColorData["AvocadoColors"][#3]& ), Epilog -> { PointSize[Large], Point[ Part[a, 3]]}, PlotRange -> All]], {a, %}]}, Spacings -> 2]
Out[10]=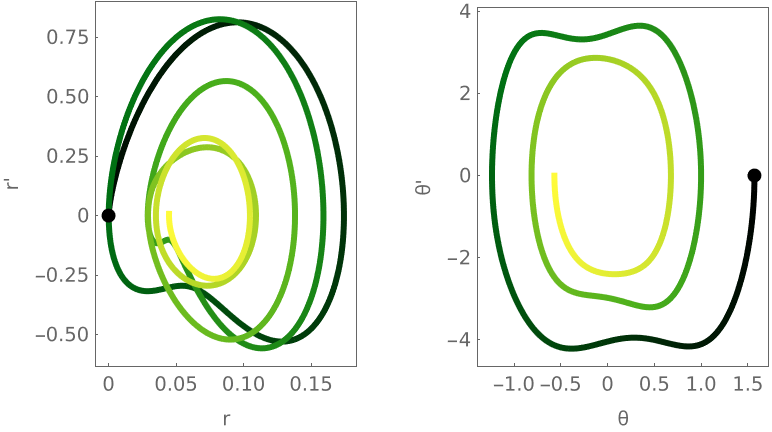

Suba Thomas, "Elastic Pendulum Model" from the Wolfram Data Repository (2025)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • P. Pokorny, "Control of Stability of Nonlinear Elastic Pendulum," in Proceedings of the 6th European Nonlinear Dynamics Conference (ENOC-2008), Saint Petersburg, Russia, Jun. 30–Jul. 4, 2008.

Publisher Information

  • Prepared for the Wolfram Data Repository By: Maher Kuzbari, Suba Thomas
  • Publisher of Record: Suba Thomas