Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Satellite Roll and Yaw Model

Model of a satellite's roll and yaw dynamics

Examples

Basic Examples (3) 

Retrieve the model:

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Satellite Roll and Yaw Model\>\"", #& , BoxID -> "ResourceTag-Satellite Roll and Yaw Model-Input", AutoDelete->True]\)]
Out[1]=

The icon:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<Satellite Roll and Yaw Model\>\"", #& , BoxID -> "ResourceTag-Satellite Roll and Yaw Model-Input", AutoDelete->True]\), "Icon"]
Out[2]=

The annotation:

In[3]:=
ResourceData[\!\(\* TagBox["\"\<Satellite Roll and Yaw Model\>\"", #& , BoxID -> "ResourceTag-Satellite Roll and Yaw Model-Input", AutoDelete->True]\), "Annotation"]
Out[3]=

Scope & Additional Elements (4) 

Available content elements:

In[4]:=
\!\(\* TagBox[ RowBox[{"ResourceObject", "[", "\"\<Satellite Roll and Yaw Model\>\"", "]"}], #& , BoxID -> "ResourceTag-Satellite Roll and Yaw Model-Input", AutoDelete->True]\)["ContentElements"]
Out[4]=

The available model types:

In[5]:=
ResourceData[\!\(\* TagBox["\"\<Satellite Roll and Yaw Model\>\"", #& , BoxID -> "ResourceTag-Satellite Roll and Yaw Model-Input", AutoDelete->True]\), "AvailableModelTypes"]
Out[5]=

The operating point:

In[6]:=
ResourceData[\!\(\* TagBox["\"\<Satellite Roll and Yaw Model\>\"", #& , BoxID -> "ResourceTag-Satellite Roll and Yaw Model-Input", AutoDelete->True]\), "OperatingPoint"]
Out[6]=

The parameters:

In[7]:=
ResourceData[\!\(\* TagBox["\"\<Satellite Roll and Yaw Model\>\"", #& , BoxID -> "ResourceTag-Satellite Roll and Yaw Model-Input", AutoDelete->True]\), "Parameters"]
Out[7]=

Analysis (11) 

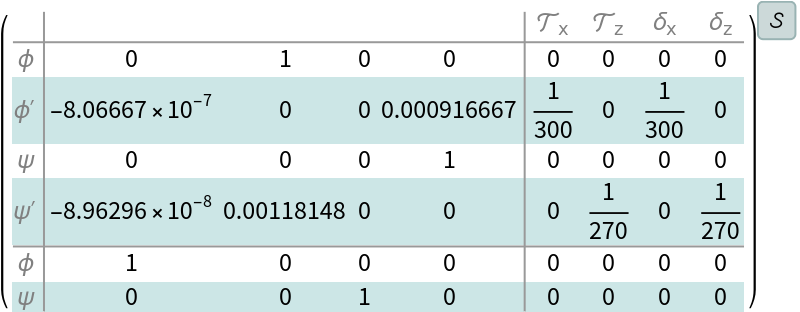
The numerical model:

In[8]:=
sat = ResourceData[\!\(\* TagBox["\"\<Satellite Roll and Yaw Model\>\"", #& , BoxID -> "ResourceTag-Satellite Roll and Yaw Model-Input", AutoDelete->True]\)] /. ResourceData[\!\(\* TagBox["\"\<Satellite Roll and Yaw Model\>\"", #& , BoxID -> "ResourceTag-Satellite Roll and Yaw Model-Input", AutoDelete->True]\), "Parameters"]
Out[8]=

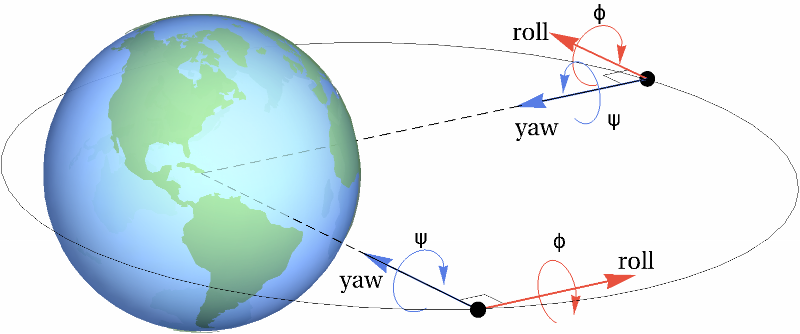
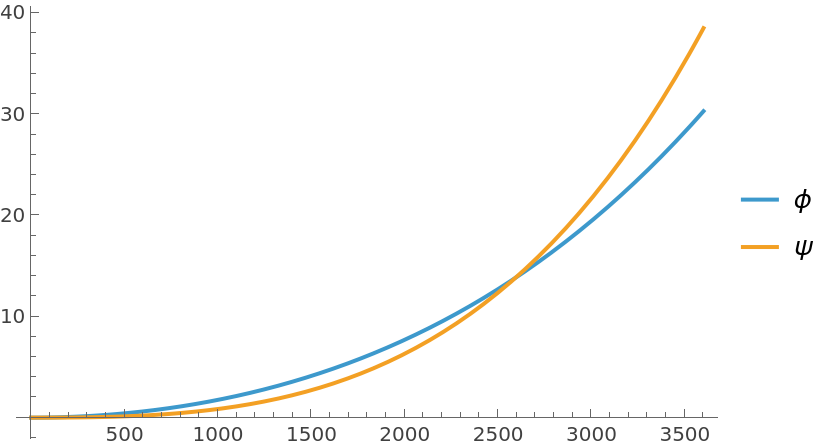
The satellite's roll and yaw angles are unregulated if disturbed:

In[9]:=
OutputResponse[sat, {0, 0, 10^-3, 10^-4}, {t, 0, 3600}]; Plot[%, {t, 0, 3600}, PlotRange -> All, PlotLegends -> {"\[Phi]", "\[Psi]"}]
Out[10]=
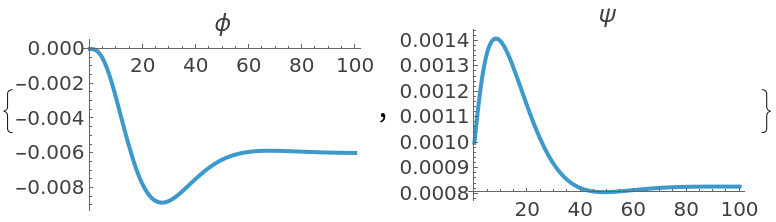
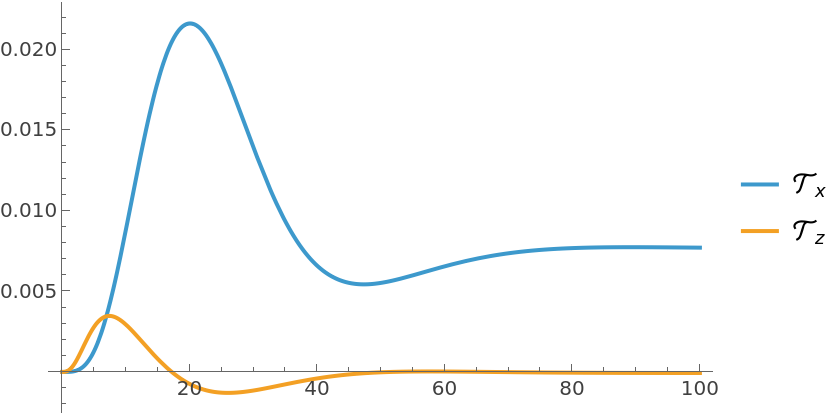
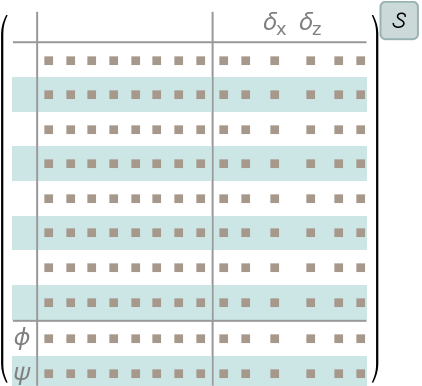
The system specification for a controller design:
In[11]:=
sspec = <|"InputModel" -> sat, "FeedbackInputs" -> {1, 2}|>;
A set of covariance and weight matrices:
In[12]:=
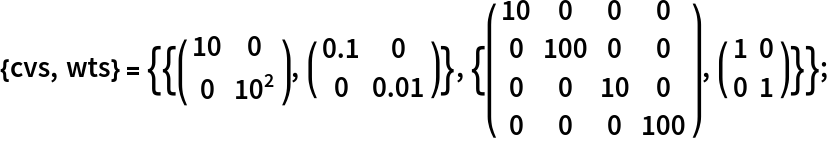
{cvs, wts} = {{({ {10, 0}, {0, 10^2} }), ({ {0.1, 0}, {0, 0.01} })}, {( { {10, 0, 0, 0}, {0, 100, 0, 0}, {0, 0, 10, 0}, {0, 0, 0, 100} }), ({ {1, 0}, {0, 1} })}};
Compute an LQG regulator:
In[13]:=
lqg = LQGRegulator[sspec, cvs, wts, "Data"]
Out[13]=
The closed-loop system:
In[14]:=
csys = lqg["ClosedLoopSystem"]
Out[14]=
A noisy signal to simulate the process noise:
In[15]:=
n = 100;
In[16]:=
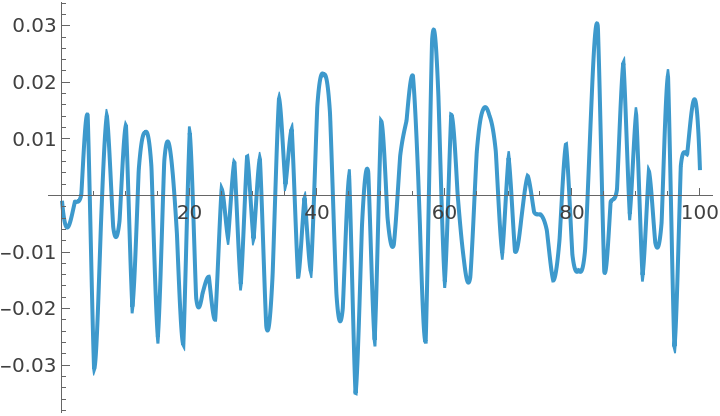
Thread[{Range[0, n], RandomVariate[NormalDistribution[0, Sqrt[2 10^-4]], {n + 1}]}]; Plot[Subscript[u, w] = Interpolation[%, t], {t, 0, n}]
Out[17]=
Another one for the sensor noise:
In[18]:=
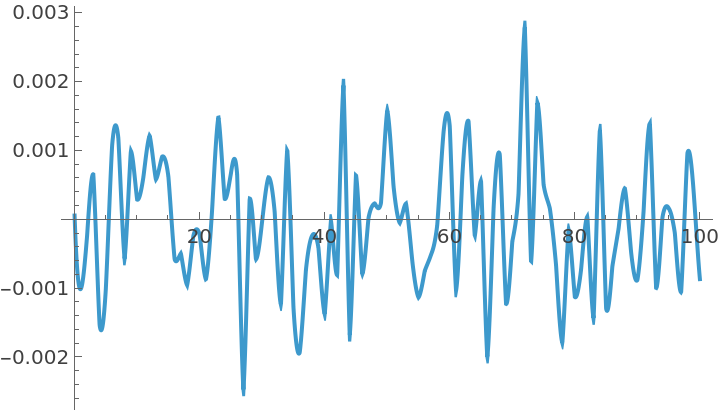
Thread[{Range[0, n], RandomVariate[NormalDistribution[0, Sqrt[10^-6]], {n + 1}]}]; Plot[Subscript[y, v] = Interpolation[%, t], {t, 0, n}]
Out[19]=
The satellite's orbit is regulated by the controller:
In[20]:=
sr = StateResponse[{csys, {0, 0, 10^-3, 10^-4}}, {0, 0, 0, 0, Subscript[u, w], Subscript[y, v]}, {t, 0, 100}]; Table[Plot[\[ScriptS]\[ScriptR][[1]], {t, 0, 100}, Sequence[ PlotLabel -> Part[\[ScriptS]\[ScriptR], 2], PlotRange -> All, ImageSize -> Small]], {\[ScriptS]\[ScriptR], ({sr[[{1, 3}]], {\[Phi], \[Psi]}}\[Transpose])}]
Out[21]=
Obtain the controller model:
In[22]:=
cm = lqg["ControllerModel"]
Out[22]=
The control effort:
In[23]:=
OutputResponse[cm, Join[{0, 0}, sr[[1 ;; 3]]], {t, 0, 100}]; Plot[%, {t, 0, 100}, PlotRange -> All, PlotLegends -> {"\!\(\*SubscriptBox[\(\[ScriptCapitalT]\), \(x\)]\)", "\!\(\*SubscriptBox[\(\[ScriptCapitalT]\), \(z\)]\)"}]
Out[24]=

Suba Thomas, "Satellite Roll and Yaw Model" from the Wolfram Data Repository (2025)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • A. E. Bryson Jr., "Control of Spacecraft and Aircraft. Princeton", NJ: Princeton University Press, 1994.

Publisher Information

  • Prepared for the Wolfram Data Repository By: Maher Kuzbari, Suba Thomas
  • Publisher of Record: Suba Thomas