Examples
Basic Examples (3)
Retrieve the model:
The icon:
The annotation:
Scope & Additional Elements (4)
Available content elements:
The available model types:
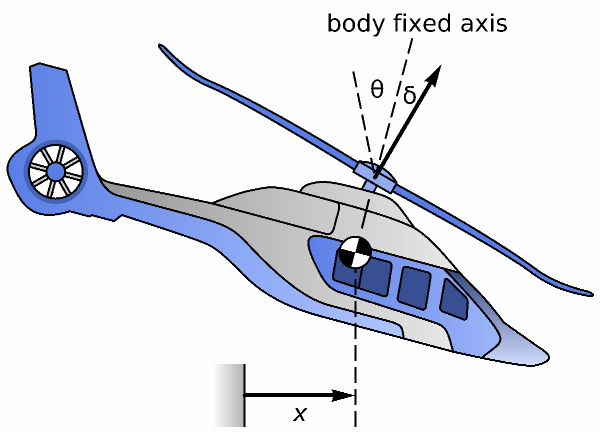
The operating point:
The parameters:
Analysis (5)
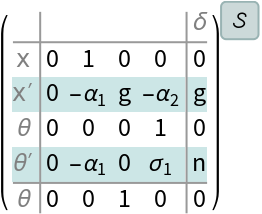
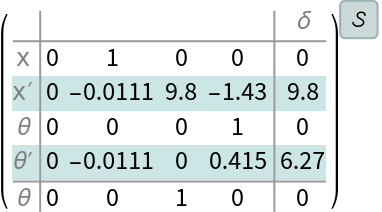
The numerical state-space model:
It's unstable:
An LQ regulator controller that stabilizes the helicopter:
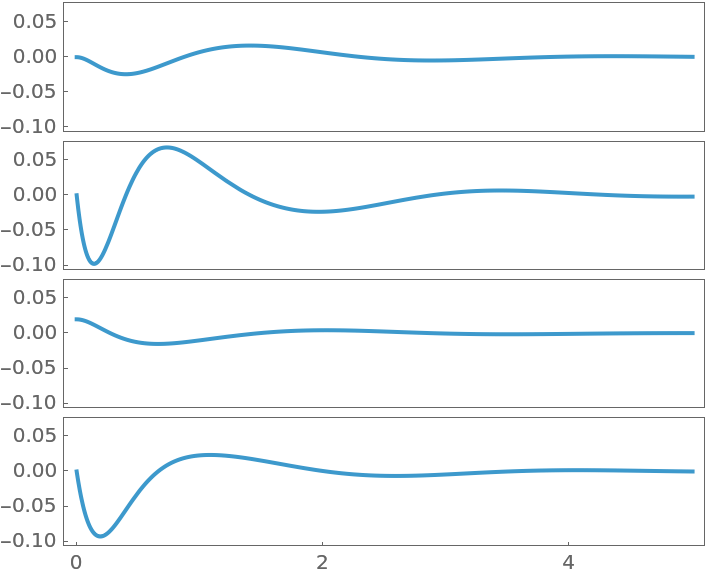
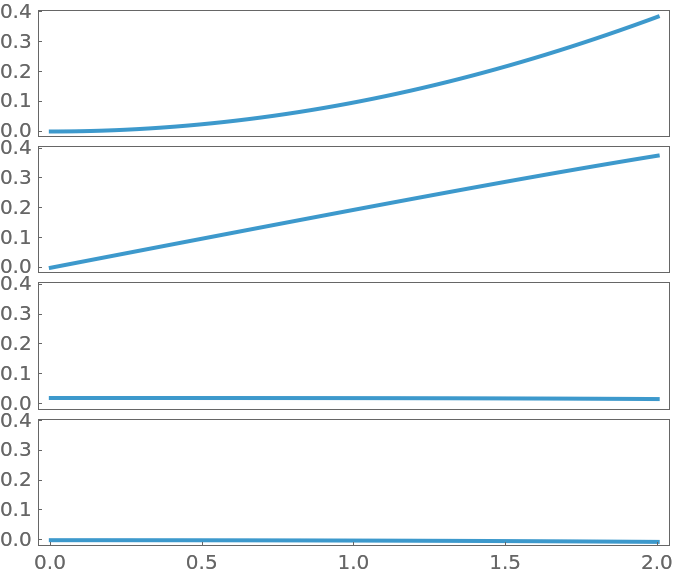
The closed-loop system is stable:
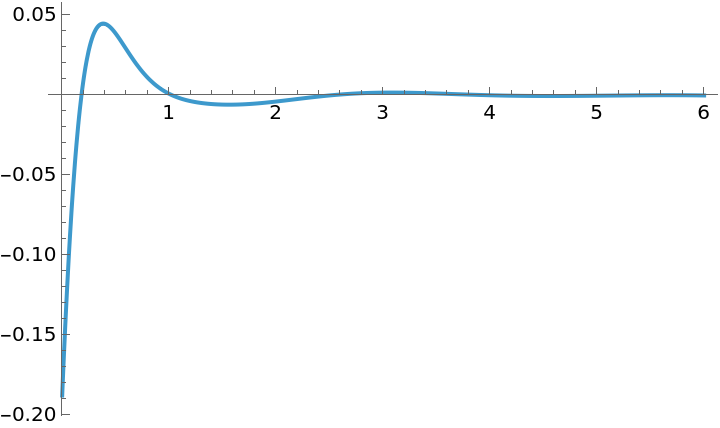
The control effort:
Bibliographic Citation
Suba Thomas,
"Helicopter Pitch Model"
from the Wolfram Data Repository
(2025)
Data Resource History
Publisher Information



![cd = LQRegulatorGains[helicopter, {({
{10^4, 0, 0, 0},
{0, 10, 0, 0},
{0, 0, 10^4, 0},
{0, 0, 0, 1}
}), {{10^3}}}, "Data"]](https://www.wolframcloud.com/obj/resourcesystem/images/559/559ebece-cd41-4e0b-a1d0-041f9aa62405/12b1bb7dd2a93c8f.png)