Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Segway Pendulum Model

Source Notebook

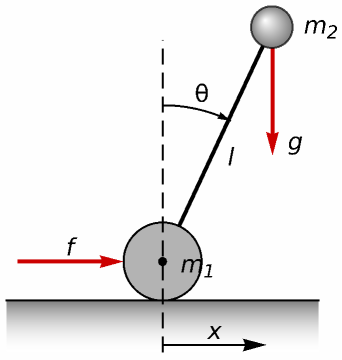
An inverted pendulum model of a Segway personal transport

Examples

Basic Examples (2) 

Retrieve the model:

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Segway Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Segway Pendulum Model-Input", AutoDelete->True]\)]
Out[1]=

The icon:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<Segway Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Segway Pendulum Model-Input", AutoDelete->True]\), "Icon"]
Out[2]=

Available content elements:

In[3]:=
\!\(\* TagBox[ RowBox[{"ResourceObject", "[", "\"\<Segway Pendulum Model\>\"", "]"}], #& , BoxID -> "ResourceTag-Segway Pendulum Model-Input", AutoDelete->True]\)["ContentElements"]
Out[3]=

The available model types:

In[4]:=
ResourceData[\!\(\* TagBox["\"\<Segway Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Segway Pendulum Model-Input", AutoDelete->True]\), "AvailableModelTypes"]
Out[4]=

The operating point:

In[5]:=
ResourceData[\!\(\* TagBox["\"\<Segway Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Segway Pendulum Model-Input", AutoDelete->True]\), "OperatingPoint"]
Out[5]=

The parameters:

In[6]:=
ResourceData[\!\(\* TagBox["\"\<Segway Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Segway Pendulum Model-Input", AutoDelete->True]\), "Parameters"]
Out[6]=

A numerical model of the system:

In[7]:=
assm = AffineStateSpaceModel[Simplify[ResourceData[\!\(\* TagBox["\"\<Segway Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Segway Pendulum Model-Input", AutoDelete->True]\)] /. ResourceData[\!\(\* TagBox["\"\<Segway Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Segway Pendulum Model-Input", AutoDelete->True]\), "Parameters"]], Automatic, Automatic, Automatic, None]
Out[7]=

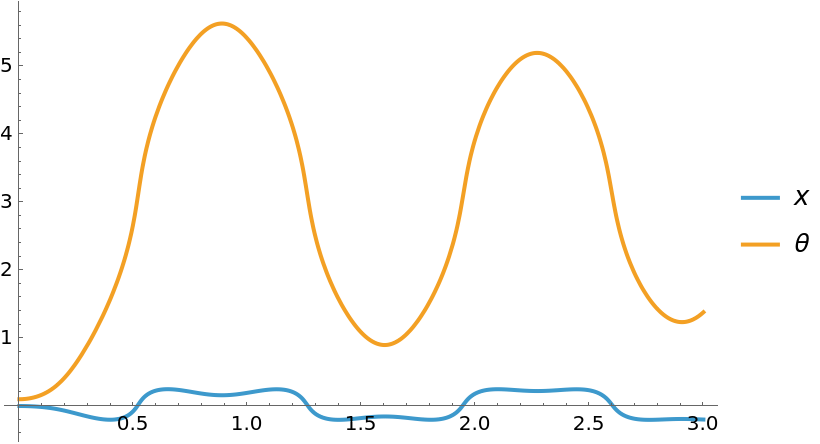
Without a controller, the Segway's position and orientation are not balanced:

In[8]:=
OutputResponse[{assm, {0.1}}, 0, {t, 0, 3}]; Plot[%, {t, 0, 3}, PlotRange -> All, PlotLegends -> {x, \[Theta]}]
Out[9]=

Balance the Segway using a pole-placement:

In[10]:=
csys = StateFeedbackGains[assm, {-3 + 0.25 I, -3 - 0.25 I, -2, -4.5}, "ClosedLoopSystem"]
Out[10]=

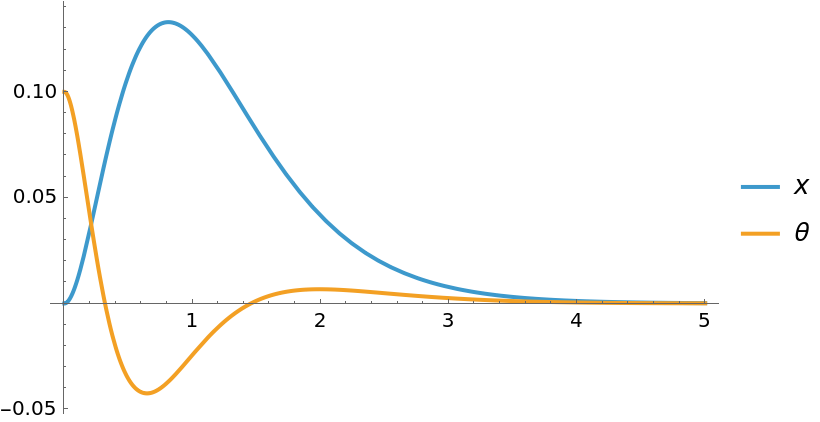
The Segway remains balance despite the disturbance:

In[11]:=
OutputResponse[{csys, {0.1}}, 0, {t, 0, 5}]; Plot[%, {t, 0, 5}, PlotRange -> All, PlotLegends -> {x, \[Theta]}]
Out[12]=

Suba Thomas, "Segway Pendulum Model" from the Wolfram Data Repository (2025)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • K. J. Åström and R. M. Murray, "Feedback Systems: An Introduction for Scientists and Engineers", Princeton Univ. Press, 2008.

Publisher Information

  • Prepared for the Wolfram Data Repository By: Maher Kuzbari, Suba Thomas
  • Publisher of Record: Suba Thomas