Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Double Pendulum Model

Source Notebook

Model of a double pendulum

Examples

Basic Examples (2) 

Retrieve the model:

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Double Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Double Pendulum Model-Input", AutoDelete->True]\)]
Out[1]=

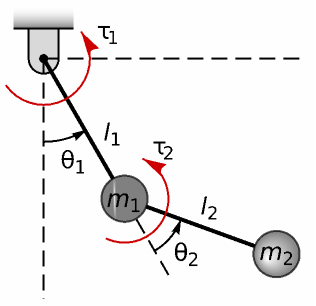
The icon:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<Double Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Double Pendulum Model-Input", AutoDelete->True]\), "Icon"]
Out[2]=

Scope & Additional Elements (4) 

Available content elements:

In[3]:=
\!\(\* TagBox[ RowBox[{"ResourceObject", "[", "\"\<Double Pendulum Model\>\"", "]"}], #& , BoxID -> "ResourceTag-Double Pendulum Model-Input", AutoDelete->True]\)["ContentElements"]
Out[3]=

The available model types:

In[4]:=
ResourceData[\!\(\* TagBox["\"\<Double Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Double Pendulum Model-Input", AutoDelete->True]\), "AvailableModelTypes"]
Out[4]=

The operating point:

In[5]:=
ResourceData[\!\(\* TagBox["\"\<Double Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Double Pendulum Model-Input", AutoDelete->True]\), "OperatingPoint"]
Out[5]=

The parameters:

In[6]:=
ResourceData[\!\(\* TagBox["\"\<Double Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Double Pendulum Model-Input", AutoDelete->True]\), "Parameters"]
Out[6]=

Visualizations (3) 

The numerical state space model:

In[7]:=
assm = ResourceData[\!\(\* TagBox["\"\<Double Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Double Pendulum Model-Input", AutoDelete->True]\)] /. ResourceData[\!\(\* TagBox["\"\<Double Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Double Pendulum Model-Input", AutoDelete->True]\), "Parameters"]
Out[7]=

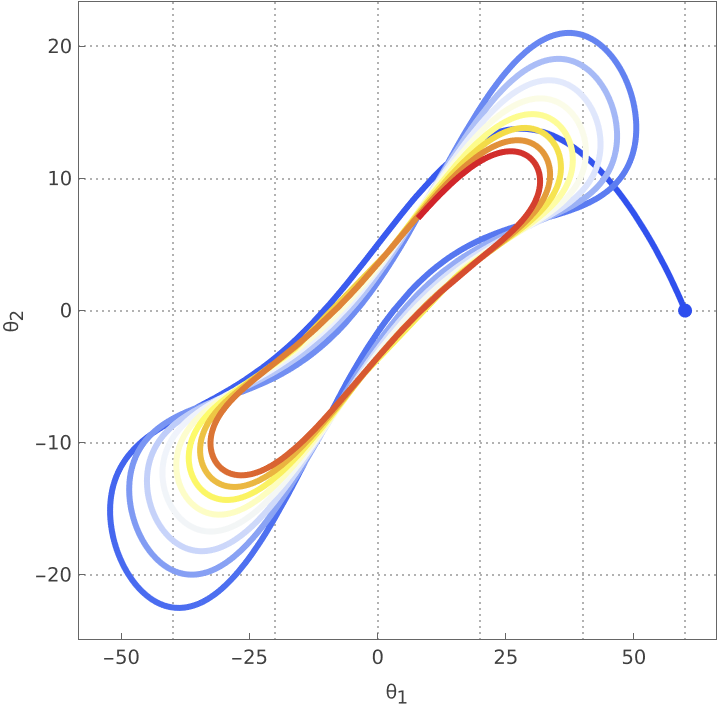
Simulate the pendulum's behaviour to some initial displacement angles:

In[8]:=
sr = StateResponse[{assm, {60 °, 0, 0, 0}}, {0, 0}, {t, 0, 60}]
Out[8]=

Plot the trajectory in the configuration space:

In[9]:=
ParametricPlot[sr[[{1, 3}]]/Degree, {t, 0, 10}, Sequence[ AspectRatio -> 1, PlotRange -> All, ColorFunction -> (ColorData["TemperatureMap"][#3]& ), PlotTheme -> "Web", GridLines -> Automatic, FrameLabel -> { Subscript[\[Theta], 1], Subscript[\[Theta], 2]}, Epilog -> { PointSize[Large], RGBColor[0.178927, 0.305394, 0.933501], Point[{59.99999999999999, 0.}]}]]
Out[9]=

Analysis (11) 

The model's equations and parameters:

In[10]:=
{eqns, pars} = assm = Table[ResourceData[\!\(\* TagBox["\"\<Double Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Double Pendulum Model-Input", AutoDelete->True]\), elems], {elems, {"Equations", "Parameters"}}]
Out[10]=

An operating point about the inverted position:

In[11]:=
opPt = Join[{Subscript[\[Theta], 1][t] -> \[Pi], Subscript[\[Theta], 2][t] -> 0}, Thread[inps -> 0]]
Out[11]=

Compute a numerical model for the new operating point:

In[12]:=
assm = AffineStateSpaceModel[eqns /. pars, opPt[[;; 2]], opPt[[3 ;;]], {Subscript[\[Theta], 1][t], Subscript[\[Theta], 2][t]}, t]
Out[12]=

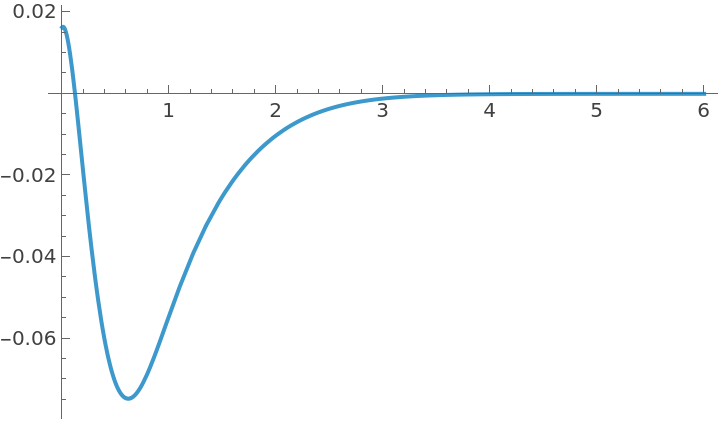
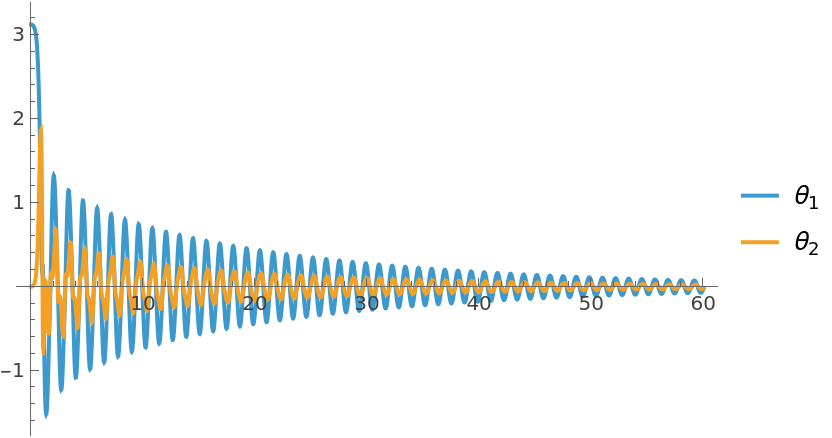
Its output response to a small deviation from the new equilibrium position:

In[13]:=
or = OutputResponse[{assm, {\[Pi] - 1 °}}, {0, 0}, {t, 0, 60}]
Out[13]=

The pendulum settles in its downward stable position:

In[14]:=
Plot[or, {t, 0, 60}, PlotRange -> All, PlotLegends -> {Subscript[\[Theta], 1], Subscript[\[Theta], 2]}]
Out[14]=

The inverted double pendulum can be balanced using only τ1:

In[15]:=
ControllableModelQ[SystemsModelExtract[assm, 1]]
Out[15]=

A specification for the controller design:

In[16]:=
assm = AffineStateSpaceModel[assm, Automatic, Automatic, Automatic, None];
In[17]:=
sspec = <|"InputModel" -> assm, "FeedbackInputs" -> 1|>;

A state feedback controller:

In[18]:=
cd = StateFeedbackGains[ sspec, {-5 + I/3, -5 - I/3, -3 + I/10, -3 - I/10}, "Data"]
Out[18]=

Simulate the closed-loop system:

In[19]:=
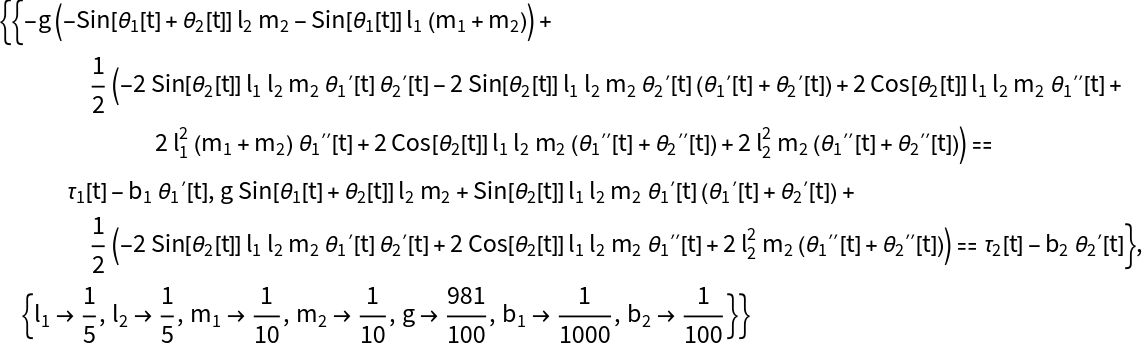
ior = InputOutputResponse[{cd[{"ClosedLoopSystem", <| "Merge" -> False|>}], {\[Pi] - 1 °}}, {0, 0}, {t, 0, 60}, "Data"]
Out[19]=

The pendulum is balanced in the upright position by the controller:

In[20]:=
Grid[{Table[ Plot[r[[1]], {t, 0, 6}, PlotRange -> All, PlotLabel -> r[[2]]], {r, {ior["OutputResponse"]/Degree, {Subscript[\[Theta], 1], Subscript[\[Theta], 2]}}\[Transpose]}]}, Spacings -> {3, 0}]
Out[20]=

The control effort:

In[21]:=
Plot[ior["SubsystemOutputResponse"][[5]], {t, 0, 6}, PlotRange -> All]
Out[21]=

Suba Thomas, "Double Pendulum Model" from the Wolfram Data Repository (2025)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • R. B. Levien and S. M. Tan, "Double pendulum: An experiment in chaos", American Journal of Physics, vol. 61, no. 11, pp. 1038–1044, Nov. 1993.

Publisher Information

  • Prepared for the Wolfram Data Repository By: Maher Kuzbari, Suba Thomas
  • Publisher of Record: Suba Thomas