Wolfram Data Repository
Immediate Computable Access to Curated Contributed Data
Substitution tiling systems based on algebraic barycentric coordinates
Data for the Pinwheel tiling:
| In[1]:= |
| Out[1]= |  |
Currently available substitution tilings:
| In[2]:= |
| Out[2]= |  |
The roots, based on SqrtSpace, with 1.47, 1.32 and 1.84 being the supergolden ratio, plastic constant and tribonacci constant:
| In[3]:= |
| Out[3]= |  |
The psi quad tiling, with the root being psi, ψ, the supergolden ratio:
| In[4]:= |
| Out[4]= |  |
The points of the psi quad tiling after algebraic conversion with SqrtSpace:
| In[5]:= |
| Out[5]= |  |
Show the points:
| In[6]:= | ![Graphics[{EdgeForm[Black], White, Polygon[pts[[#]]] & /@ ps["PolygonReplacementRules"][[1, 2]], Green,
Opacity[.2], Polygon[pts[[{1, 2, 3, 4}]]], Opacity[1], Black, Table[Style[Text[n, pts[[n]]], 20], {n, 1, 6}]}, ImageSize -> Small]](https://www.wolframcloud.com/obj/resourcesystem/images/67d/67d43f66-305c-44f4-87b1-4af258a41cb9/1729d35e2f997702.png) |
| Out[6]= | 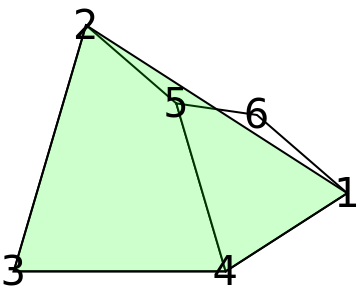 |
Data for the Kites and Darts tiling system:
| In[7]:= |
| Out[7]= |  |
Using AlgebraicSubstitutionTiling, show the substitution rule and three steps:
| In[8]:= | ![Row[Table[
ResourceFunction["AlgebraicSubstitutionTiling"][{kd["Root"], kd["AlgebraicPointList"], kd["PolygonReplacementRules"], kd["PolygonType"]}, k], {k, 0, 3}]]](https://www.wolframcloud.com/obj/resourcesystem/images/67d/67d43f66-305c-44f4-87b1-4af258a41cb9/3ae5bf533bb4f268.png) |
| Out[8]= | 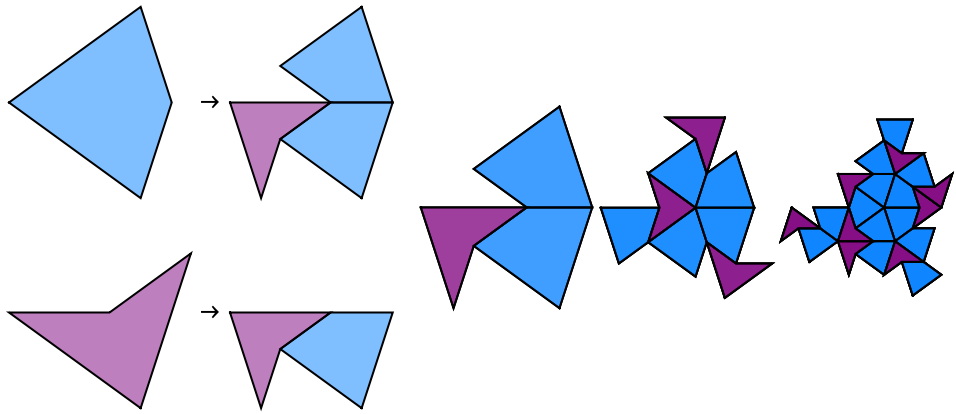 |
Wolfram Research, "Algebraic Substitution Tilings" from the Wolfram Data Repository (2022)