Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Ant Nests

Source Notebook

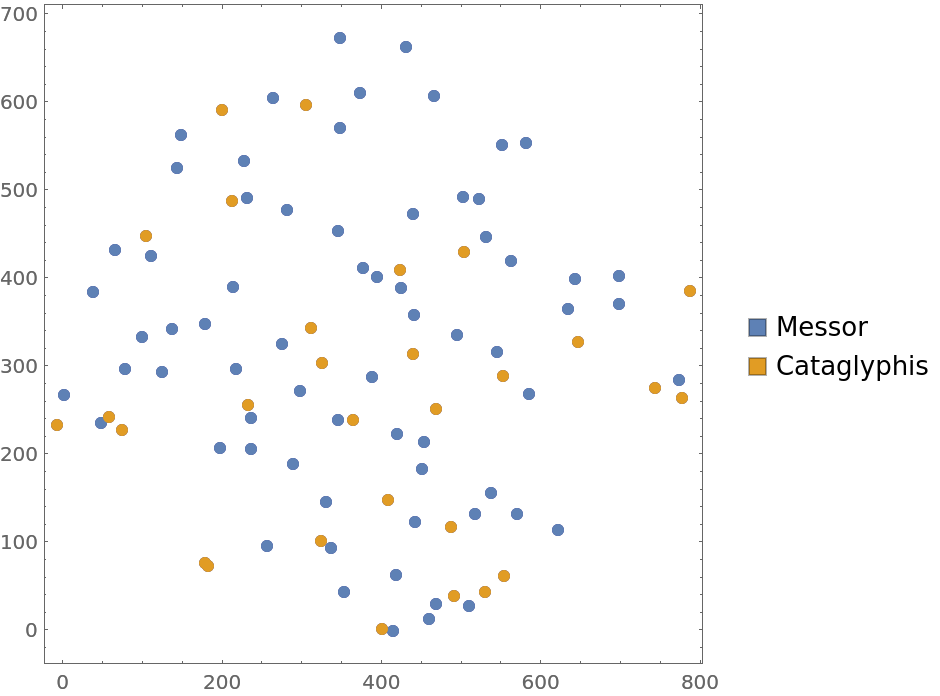
Locations of ant nests with marks denoting two types of species

Details

Locations of ant nests in the observation region Rectangle[{-7, -1}, {787, 673}] in feet, annotated with species Cataglyphis/Messor.

Examples

Basic Examples (3) 

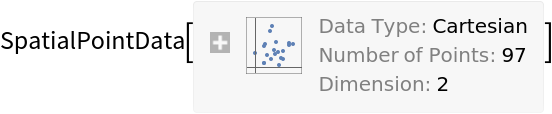
Retrieve the data:

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Ant Nests\>\"", #& , BoxID -> "ResourceTag-Ant Nests-Input", AutoDelete->True]\)]
Out[1]=

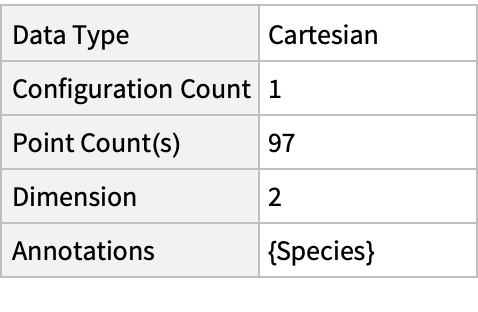
Summary of the spatial point data:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<Ant Nests\>\"", #& , BoxID -> "ResourceTag-Ant Nests-Input", AutoDelete->True]\), "Data"]["Summary"]
Out[2]=

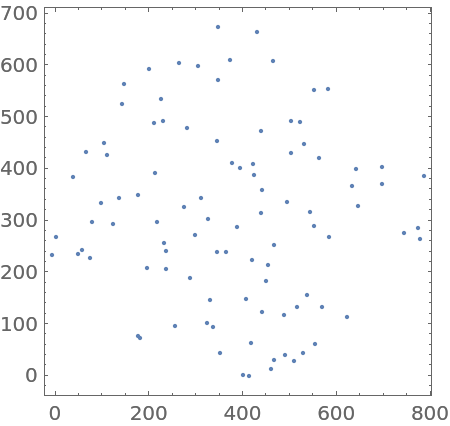
Plot the points:

In[3]:=
ListPlot[ResourceData[\!\(\* TagBox["\"\<Ant Nests\>\"", #& , BoxID -> "ResourceTag-Ant Nests-Input", AutoDelete->True]\), "Data"], Frame -> True, AspectRatio -> 1]
Out[3]=

Scope & Additional Elements (1) 

Select subsets based on the species type:

In[4]:=
messor = SpatialPointSelect[ResourceData[\!\(\* TagBox["\"\<Ant Nests\>\"", #& , BoxID -> "ResourceTag-Ant Nests-Input", AutoDelete->True]\), "Data"], #Species == "Messor" &]
Out[4]=
In[5]:=
cataglyphis = SpatialPointSelect[ResourceData[\!\(\* TagBox["\"\<Ant Nests\>\"", #& , BoxID -> "ResourceTag-Ant Nests-Input", AutoDelete->True]\), "Data"], #Species == "Cataglyphis" &]
Out[5]=

Visualizations (1) 

Plot locations with information about species:

In[6]:=
PointValuePlot[ResourceData[\!\(\* TagBox["\"\<Ant Nests\>\"", #& , BoxID -> "ResourceTag-Ant Nests-Input", AutoDelete->True]\), "Data"], PlotLegends -> Automatic]
Out[6]=

Analysis (4) 

Test for complete spacial randomness:

In[7]:=
SpatialRandomnessTest[ResourceData[\!\(\* TagBox["\"\<Ant Nests\>\"", #& , BoxID -> "ResourceTag-Ant Nests-Input", AutoDelete->True]\), "Data"], {"PValue", "TestConclusion"}]
Out[7]=

Fit a hard core point process to data:

In[8]:=
EstimatedPointProcess[ResourceData[\!\(\* TagBox["\"\<Ant Nests\>\"", #& , BoxID -> "ResourceTag-Ant Nests-Input", AutoDelete->True]\), "Data"], HardcorePointProcess[\[Mu], r, 2]]
Out[8]=

Compute probability of finding a point within given radius of an existing point - NearestNeighborG is the CDF of the nearest neighbor distribution:

In[9]:=
nnG = NearestNeighborG[ResourceData[\!\(\* TagBox["\"\<Ant Nests\>\"", #& , BoxID -> "ResourceTag-Ant Nests-Input", AutoDelete->True]\), "Data"]]
Out[9]=
In[10]:=
DiscretePlot[nnG[r], {r, 0.01, nnG["MaxRadius"], 1}, AxesLabel -> {"radius", "probability"}]
Out[10]=

Mean distance between a typical point and its nearest neighbor (for positive support distribution can be approximated via a Riemann sum of 1-CDF):

In[11]:=
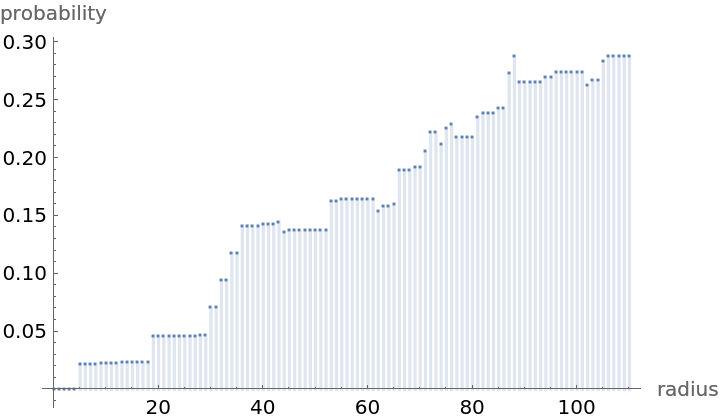
step = nnG["MaxRadius"]/100.; partition = Table[{k, k + step}, {k, 0, nnG["MaxRadius"], step}]; values = nnG[Mean /@ partition];
In[12]:=
Total[(1 - values)*step]*ResourceData[\!\(\* TagBox["\"\<Ant Nests\>\"", #& , BoxID -> "ResourceTag-Ant Nests-Input", AutoDelete->True]\), "RegionUnit"]
Out[12]=

Gosia Konwerska, "Ant Nests" from the Wolfram Data Repository (2021)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • Harkness R., Isham V. (1983). A Bivariate Spatial Point Pattern of Ants’ Nests., Applied Statistics, 32, 293-303.

Publisher Information

  • Prepared for the Wolfram Data Repository By: Gosia Konwerska (Wolfram Research, Inc.)
  • Publisher of Record: Gosia Konwerska