Cunningham Number Factorizations

Numbers of the form b^n-1 and b^n+1 are factored for small prime bases b={2,3,5,7}

For b^n-1 and b^n+1, the first table of factorizations was published by Cunningham in 1925. Through various advancement in computing power and factorization methods, the tables have been extended. The most recently found entry for the tables here are for 3^619-1 (Feb 2017). The smallest numbers with unknown factorizations are as follows:

b -1 +1

2 1207 1033

3 661 589

5 431 373

7 359 331

(5704 elements)

Examples

Basic Examples

Retrieve the resource:

In[1]:=

Out[1]=

Retrieve the default content:

In[2]:=

Out[2]=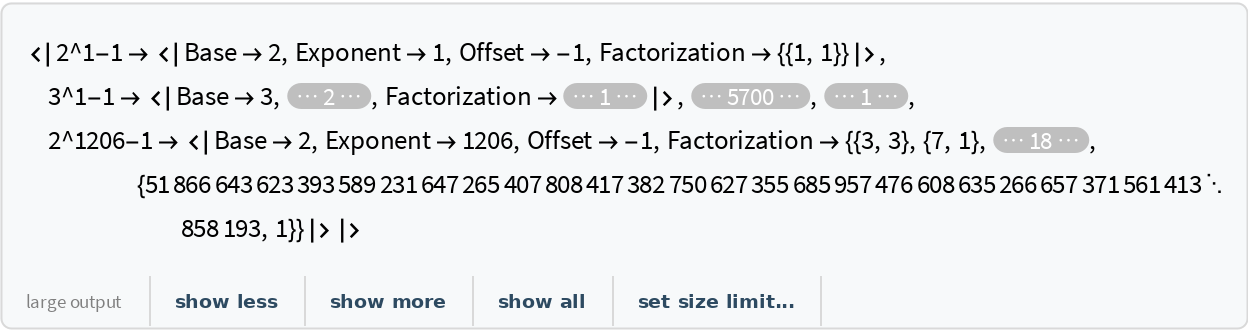

Visualization

In 1871, Aurifeuille discovered a factorization for 2^58+1:

In[3]:=

Out[3]=

Various entries are not completely factored:

In[4]:=

With[{factorizations = ResourceData["Cunningham Number Factorizations"]}, SplitBy[SortBy[
Table[If[
Not[PrimeQ[First[Last[factorizations[[n]]["Factorization"]]]]], Take[List @@ factorizations[[n]], 3], Sequence @@ {} ], {n, 2, Length[factorizations]}], {#[[1]], #[[3]], #[[2]]} &], {#[[
1]], #[[3]]} &]]

Out[4]=

Many of the factorizations have odd patterns within the digits, such as 2^995+1:

In[5]:=

$ArrayPlot[ Partition[ PadRight[Flatten[ MapIndexed[#1 Mod[#2[[1]], 2, 1] &, (IntegerDigits[#, 2] & /@ (First /@ ResourceData["Cunningham Number Factorizations"]["2^995+1"][ "Factorization"]))]], 1265], 40], ImageSize -> {500, 250}, Frame -> False, PixelConstrained -> True]$

Out[5]=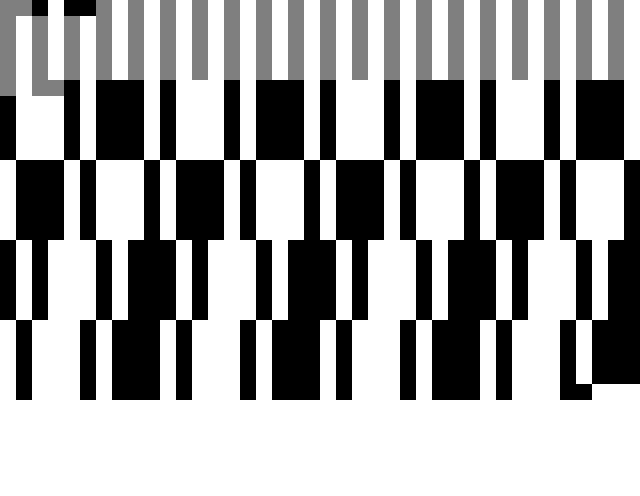

The factorization of 3^336+1 has odd patterns in ternary:

In[6]:=

$ArrayPlot[ Partition[ PadRight[Flatten[ IntegerDigits[#, 3] & /@ (First /@ ResourceData["Cunningham Number Factorizations"]["3^336+1"][ "Factorization"])], 400], 30], ImageSize -> {500, 250}, Frame -> False, PixelConstrained -> True]$

Out[6]=

Analysis

Bibliographic Citation

Wolfram Research, "Cunningham Number Factorizations" from the Wolfram Data Repository (2017) https://doi.org/10.24097/wolfram.67179.data

Data Resource History

Date Created: 2 May 2017

Source Metadata

Creator: Cunningham Project
Source: https://homes.cerias.purdue.edu/%7Essw/cun/index.html
Citation: The Cunningham Project

Data Downloads

Publisher Information

Publisher of Record: Wolfram Research