Wolfram Data Repository
Immediate Computable Access to Curated Contributed Data
Danish Fire Insurance Claims
Fire insurance claims in Denmark from Thursday 3rd January 1980 until Monday 31st December 1990
Details
These data are used in the book Modelling Extremal Events by Embrechts, Kluppelberg and Mikosch to illustrate modelling extremal events with the Pareto distribution.
Examples
Basic Examples (1)
| In[1]:= | ![ts = ResourceData["Danish Fire Insurance Claims"]](https://www.wolframcloud.com/obj/resourcesystem/images/4de/4deb3a67-d305-41c5-aa63-3e5175b36a2d/3686b26401a1e56b.png){kind=small} |
| Out[1]= |  |
Plot the data:
| In[2]:= | ![dataDanish = ts["Values"];
ListPlot[dataDanish, Sequence[
Filling -> Axis, PlotRange -> All, Axes -> False, Frame -> True, FrameLabel -> {"Time Index", "Claim Size"}, ImageSize -> 500, BaseStyle -> {FontSize -> 14}]]](https://www.wolframcloud.com/obj/resourcesystem/images/4de/4deb3a67-d305-41c5-aa63-3e5175b36a2d/4b2fcf95c131e2a8.png){kind=small} |
| Out[3]= |  |
Visualizations (1)
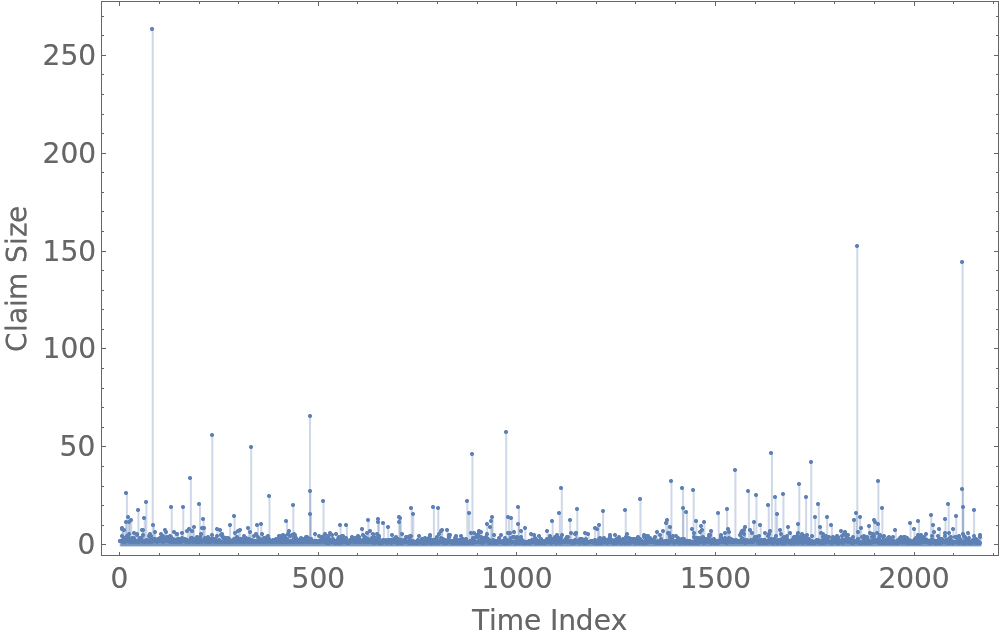Construct a histogram of the log claim size:
| In[4]:= | ![ts = ResourceData["Danish Fire Insurance Claims"];
dataDanish = ts["Values"];
Histogram[
Log[dataDanish], Sequence[{0, 4, 0.05}, PlotRange -> All, Axes -> False, Frame -> True, FrameLabel -> {"\!\(\*SubscriptBox[\(log\), \(e\)]\)(Claim Size)", "Count"}, ImageSize -> 500, BaseStyle -> {FontSize -> 14}]]](https://www.wolframcloud.com/obj/resourcesystem/images/4de/4deb3a67-d305-41c5-aa63-3e5175b36a2d/15deddc088fa8c35.png) |
| Out[6]= |  |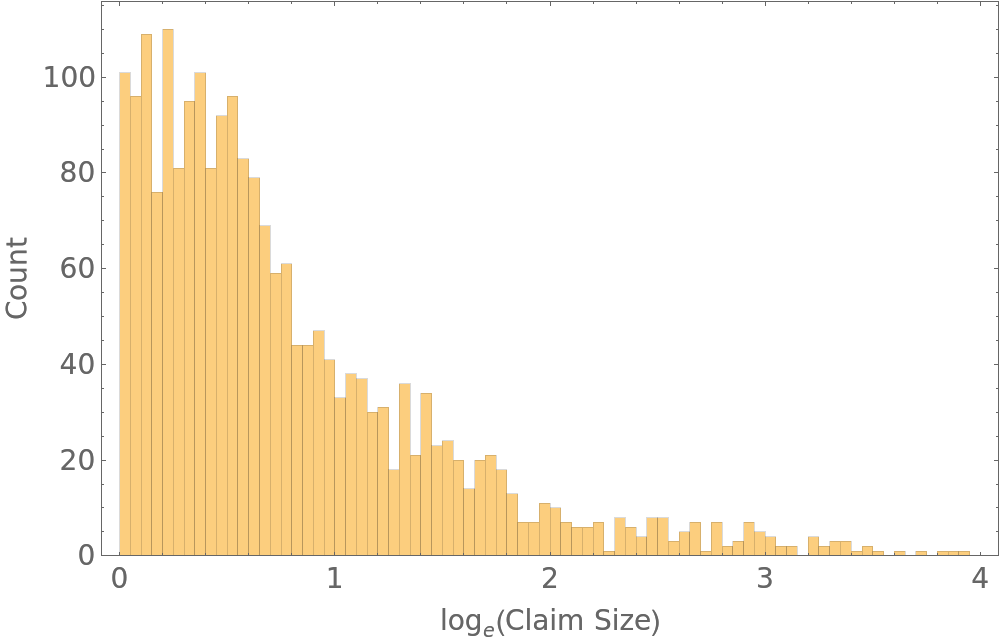
Analysis (2)
Threshold the data and fit to a Pareto distribution:
| In[7]:= | ![u = 10.0;
ts = ResourceData["Danish Fire Insurance Claims"];
dataDanish = ts["Values"];
data = Sort@Select[dataDanish, # > u &];
Nd = Length[data];
Clear[k, \[Alpha], \[Mu]];
d = EstimatedDistribution[data, ParetoDistribution[k, \[Alpha], \[Mu]]]](https://www.wolframcloud.com/obj/resourcesystem/images/4de/4deb3a67-d305-41c5-aa63-3e5175b36a2d/220968a25a4e7d85.png) |
| Out[13]= |  |
Compare empirical and theoretical cumulative probability distributions:
| In[14]:= | ![modelCDF = Table[{Log[x], CDF[d, x]}, {x, Min[data], Max[data], 0.1}];
empiricalCDF = Transpose[{Log[data], N@Table[n/Nd, {n, 1, Nd}]}];
ListPlot[empiricalCDF, Epilog -> {Line[modelCDF]}, Sequence[
Axes -> False, Frame -> True, FrameLabel -> {"\!\(\*SubscriptBox[\(log\), \(e\)]\)(Claim Size)", "Cummulative Probability Density"}, ImageSize -> 400, BaseStyle -> {FontSize -> 14}, AspectRatio -> 1]]](https://www.wolframcloud.com/obj/resourcesystem/images/4de/4deb3a67-d305-41c5-aa63-3e5175b36a2d/58d0d8c324f8188a.png) |
| Out[16]= |  |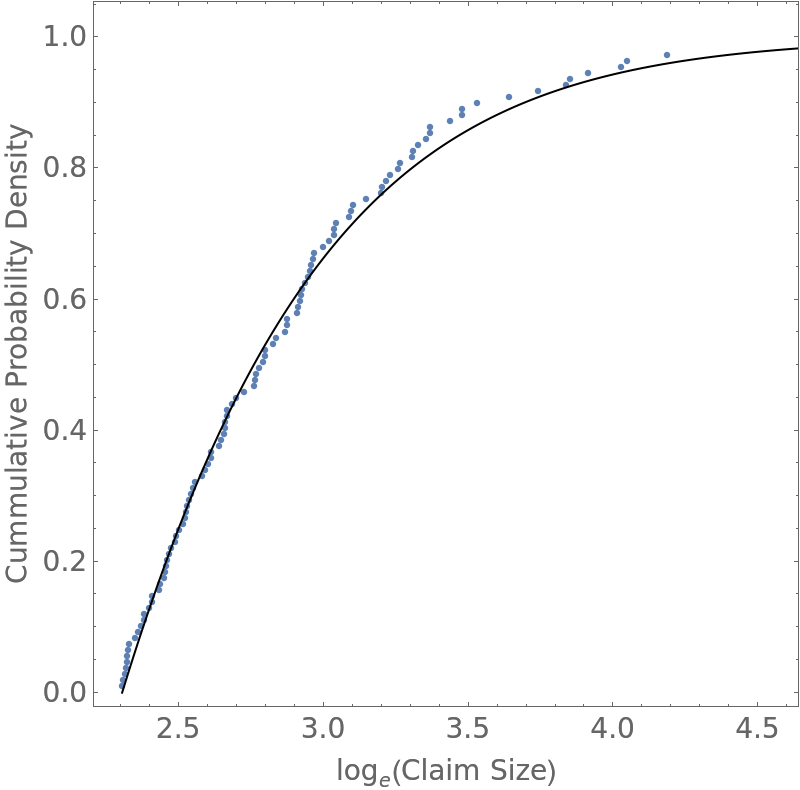
External Links
Bibliographic Citation
Marshall Bradley, "Danish Fire Insurance Claims" from the Wolfram Data Repository (2022)