Examples
Basic Examples (3)
Retrieve the graph:
Find the vertex count for the network:
Find the edge count for the network:
Visualizations (3)
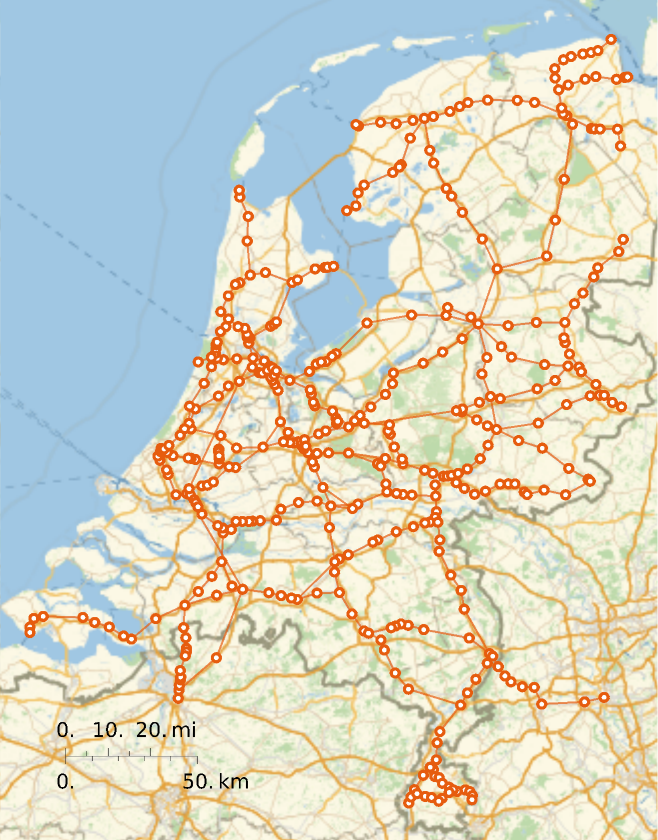
Visualize the full GeoGraphPlot:
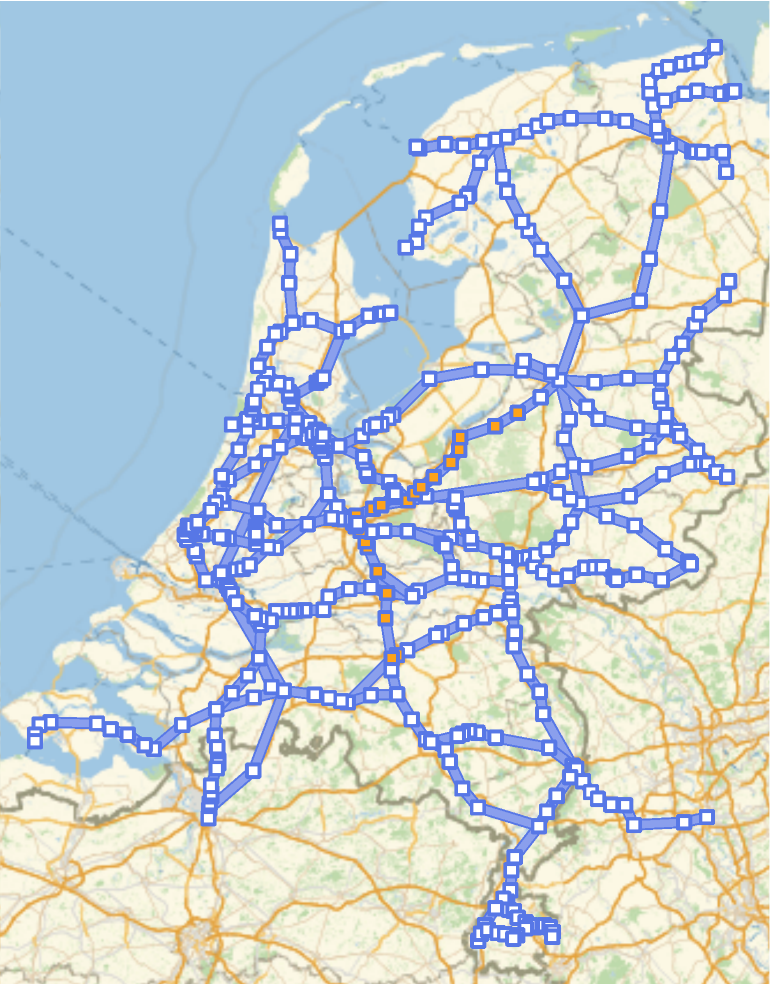
Visualize the vertices with more disruptions:
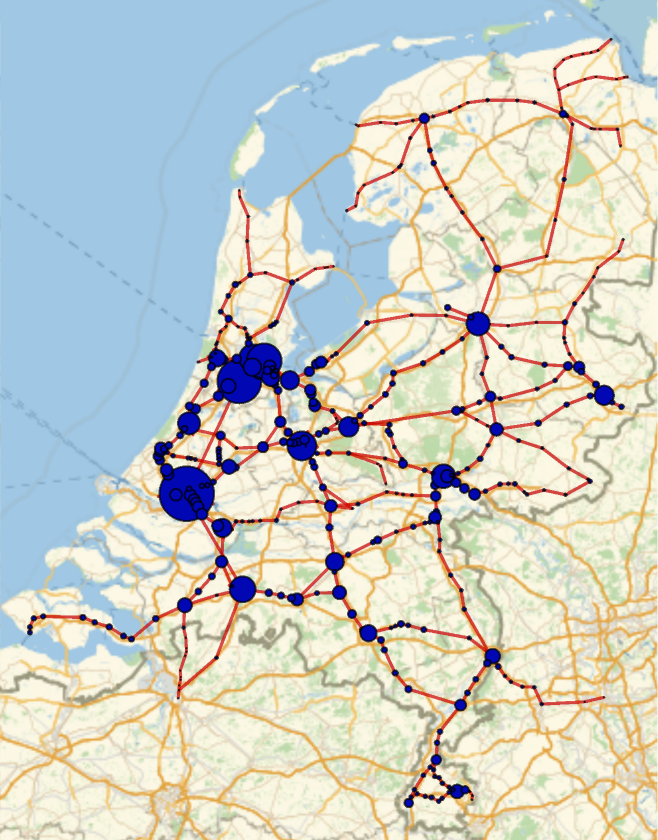
Visualize the vertices with more connections:
Analysis (2)
Find a shortest path between two stations:
And visualize the path:
Bibliographic Citation
Wolfram Discrete Computation,
"Dutch Railway Network"
from the Wolfram Data Repository
(2025)
Data Resource History
Publisher Information

![GeoGraphPlot[ResourceData[\!\(\*
TagBox["\"\<Dutch Railway Network\>\"",
#& ,
BoxID -> "ResourceTag-Dutch Railway Network-Input",
AutoDelete->True]\)] /. ResourceData[\!\(\*
TagBox["\"\<Dutch Railway Network\>\"",
#& ,
BoxID -> "ResourceTag-Dutch Railway Network-Input",
AutoDelete->True]\), "Position"], VertexSize -> 3, PlotTheme -> "Scientific"]](https://www.wolframcloud.com/obj/resourcesystem/images/8a2/8a2bfcd4-1e80-425a-8f77-ba9a97e4ee40/18f9f7791b01e2a5.png)
![GeoGraphPlot[g /. ResourceData[\!\(\*
TagBox["\"\<Dutch Railway Network\>\"",
#& ,
BoxID -> "ResourceTag-Dutch Railway Network-Input",
AutoDelete->True]\), "Position"], VertexSize -> Thread[((ResourceData[\!\(\*
TagBox["\"\<Dutch Railway Network\>\"",
#& ,
BoxID -> "ResourceTag-Dutch Railway Network-Input",
AutoDelete->True]\), "VertexWeight"][[;; , 1]]) /. ResourceData[\!\(\*
TagBox["\"\<Dutch Railway Network\>\"",
#& ,
BoxID -> "ResourceTag-Dutch Railway Network-Input",
AutoDelete->True]\), "Position"]) -> ResourceData[\!\(\*
TagBox["\"\<Dutch Railway Network\>\"",
#& ,
BoxID -> "ResourceTag-Dutch Railway Network-Input",
AutoDelete->True]\), "VertexWeight"][[;; , 2]]/30], PlotTheme -> "Classic"]](https://www.wolframcloud.com/obj/resourcesystem/images/8a2/8a2bfcd4-1e80-425a-8f77-ba9a97e4ee40/19f203f6c9a83742.png)

![sp = FindShortestPath[Graph[ResourceData[\!\(\*
TagBox["\"\<Dutch Railway Network\>\"",
#& ,
BoxID -> "ResourceTag-Dutch Railway Network-Input",
AutoDelete->True]\)], EdgeWeight -> ResourceData[\!\(\*
TagBox["\"\<Dutch Railway Network\>\"",
#& ,
BoxID -> "ResourceTag-Dutch Railway Network-Input",
AutoDelete->True]\), "EdgeWeight"]], "'s-Hertogenbosch Oost", "'t Harde"]](https://www.wolframcloud.com/obj/resourcesystem/images/8a2/8a2bfcd4-1e80-425a-8f77-ba9a97e4ee40/3ecb57d1f39ac9ce.png)

![GeoGraphPlot[HighlightGraph[ResourceData[\!\(\*
TagBox["\"\<Dutch Railway Network\>\"",
#& ,
BoxID -> "ResourceTag-Dutch Railway Network-Input",
AutoDelete->True]\)] /. ResourceData[\!\(\*
TagBox["\"\<Dutch Railway Network\>\"",
#& ,
BoxID -> "ResourceTag-Dutch Railway Network-Input",
AutoDelete->True]\), "Position"], VertexSize -> 2, GraphHighlight -> (sp /. ResourceData[\!\(\*
TagBox["\"\<Dutch Railway Network\>\"",
#& ,
BoxID -> "ResourceTag-Dutch Railway Network-Input",
AutoDelete->True]\), "Position"])], PlotTheme -> "Business", VertexSize -> 1]](https://www.wolframcloud.com/obj/resourcesystem/images/8a2/8a2bfcd4-1e80-425a-8f77-ba9a97e4ee40/432679343cf84c26.png)