Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Families of Newtonian Periodic Planar Three-Body Orbits

Source Notebook

The 695 Newtonian Periodic Planar Three-Body Orbits

Originator: X. Li, S. Liao

The three-body problem seeks solutions for the orbits of three masses under the mutual influence of gravity. Periodic solutions are very hard to find.

(695 elements)

Examples

Basic Examples

Extract velocities:

In[1]:=
ResourceData[ "Families of Newtonian Periodic Planar Three-Body Orbits"][ "I.A1"]["Velocity"]
Out[1]=

Maximum value of period:

In[2]:=
Max[AssociationMap[ ResourceData[ "Families of Newtonian Periodic Planar Three-Body Orbits"][#][ "Period"] &, Keys[ResourceData[ "Families of Newtonian Periodic Planar Three-Body Orbits"]]]]
Out[2]=

All initial velocities:

In[3]:=
Graphics[ Point[Values[ AssociationMap[ ResourceData[ "Families of Newtonian Periodic Planar Three-Body Orbits"][#1]["Velocity"] &, Keys[ResourceData[ "Families of Newtonian Periodic Planar Three-Body Orbits"]]]]], AspectRatio -> 1, Frame -> True, FrameTicks -> True]
Out[3]=

Use NBodySimulation to solve an orbit:

In[4]:=
Module[{n = 106, view = "real space"}, With[{parameters = ResourceData[ "Families of Newtonian Periodic Planar Three-Body Orbits"][ Keys[ResourceData[ "Families of Newtonian Periodic Planar Three-Body Orbits"]][[ n]]]}, Module[{data = NBodySimulation[ "InverseSquare", {<|"Mass" -> 1, "Position" -> parameters["Position"], "Velocity" -> parameters["Velocity"]|>, <|"Mass" -> 1, "Position" -> -parameters["Position"], "Velocity" -> parameters["Velocity"]|>, <|"Mass" -> 1, "Position" -> {0, 0}, "Velocity" -> -2 parameters["Velocity"]|>}, parameters["Period"]]}, ParametricPlot[ Evaluate[data[All, "Position", t]], {t, 0, parameters["Period"]}]]]]
Out[4]=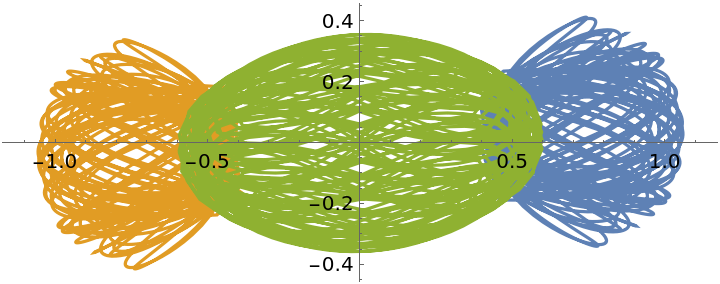

Plot in a "shape sphere" using Jacobi three-body coordinates:

In[5]:=
data = Module[{n = 106}, With[{parameters = ResourceData[ "Families of Newtonian Periodic Planar Three-Body Orbits"][ Keys[ResourceData[ "Families of Newtonian Periodic Planar Three-Body Orbits"]][[ n]]]}, Module[{data = NBodySimulation[ "InverseSquare", {<|"Mass" -> 1, "Position" -> parameters["Position"], "Velocity" -> parameters["Velocity"]|>, <|"Mass" -> 1, "Position" -> -parameters["Position"], "Velocity" -> parameters["Velocity"]|>, <|"Mass" -> 1, "Position" -> {0, 0}, "Velocity" -> -2 parameters["Velocity"]|>}, parameters["Period"]]}, data]]]
Out[5]=
In[6]:=
Show[ParametricPlot3D[{(((x1 - x2) (x1 + x2 - 2 x3))/Sqrt[ 3] + ((y1 - y2) (y1 + y2 - 2 y3))/Sqrt[3])/( 1/2 (x1 - x2)^2 + 1/6 (x1 + x2 - 2 x3)^2 + 1/2 (y1 - y2)^2 + 1/6 (y1 + y2 - 2 y3)^2), (-(1/2) (x1 - x2)^2 + 1/6 (x1 + x2 - 2 x3)^2 - 1/2 (y1 - y2)^2 + 1/6 (y1 + y2 - 2 y3)^2)/( 1/2 (x1 - x2)^2 + 1/6 (x1 + x2 - 2 x3)^2 + 1/2 (y1 - y2)^2 + 1/6 (y1 + y2 - 2 y3)^2), ( 2 (-(((x1 + x2 - 2 x3) (y1 - y2))/( 2 Sqrt[3])) + ((x1 - x2) (y1 + y2 - 2 y3))/(2 Sqrt[3])))/( 1/2 (x1 - x2)^2 + 1/6 (x1 + x2 - 2 x3)^2 + 1/2 (y1 - y2)^2 + 1/6 (y1 + y2 - 2 y3)^2)} /. Thread[{x1, y1, x2, y2, x3, y3} -> Flatten[data[All, "Position", t]]], {t, 0, 32.2}, BoxRatios -> 1, PlotRange -> All, AspectRatio -> 1, PlotStyle -> Yellow, MaxRecursion -> 9, Axes -> False, ImageSize -> 445, Boxed -> False, SphericalRegion -> True, Background -> Black], Graphics3D[{Red, PointSize[.03], Point[{{-(Sqrt[3]/2), -(1/2), 0}, {Sqrt[3]/2, -(1/2), 0}, {0, 1, 0}}], Opacity[.35], Green, Sphere[]}]]
Out[6]=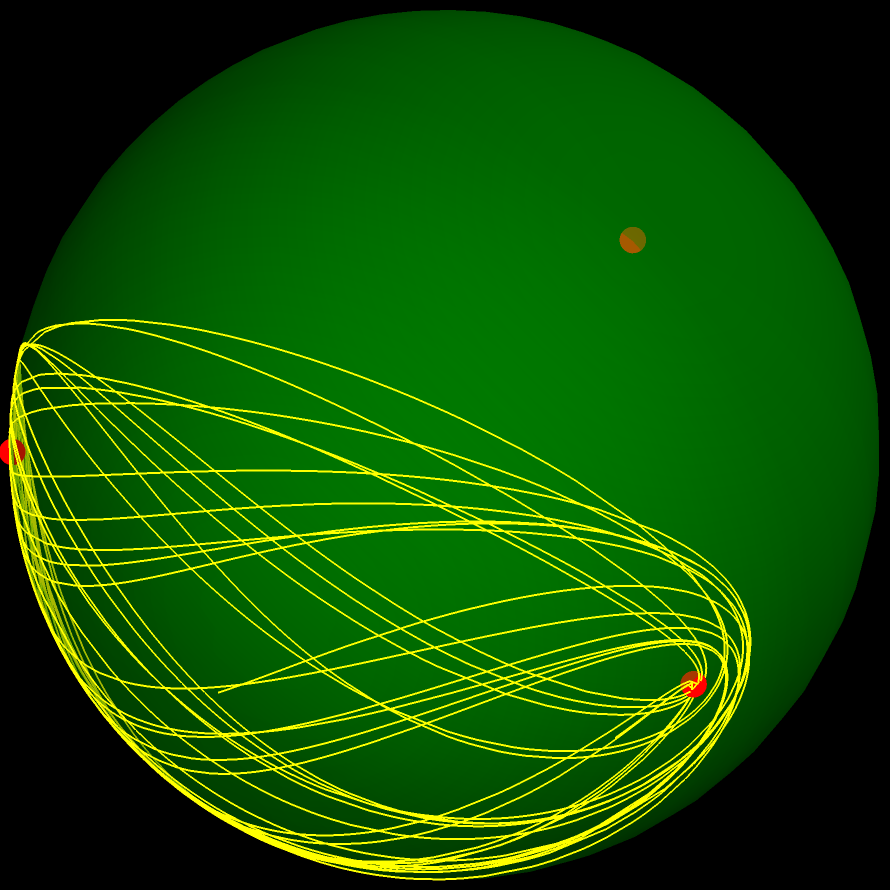

Plot orbits from different families:

In[7]:=
Table[With[{parameters = ResourceData[ "Families of Newtonian Periodic Planar Three-Body Orbits"][n]}, Module[{data = NBodySimulation[ "InverseSquare", {<|"Mass" -> 1, "Position" -> parameters["Position"], "Velocity" -> parameters["Velocity"]|>, <|"Mass" -> 1, "Position" -> -parameters["Position"], "Velocity" -> parameters["Velocity"]|>, <|"Mass" -> 1, "Position" -> {0, 0}, "Velocity" -> -2 parameters["Velocity"]|>}, parameters["Period"]]}, ParametricPlot[ Evaluate[data[All, "Position", t]], {t, 0, parameters["Period"]}]]], {n, {"I.A1", "I.B1", "II.A1", "II.B1", "II.C1"}}]
Out[7]=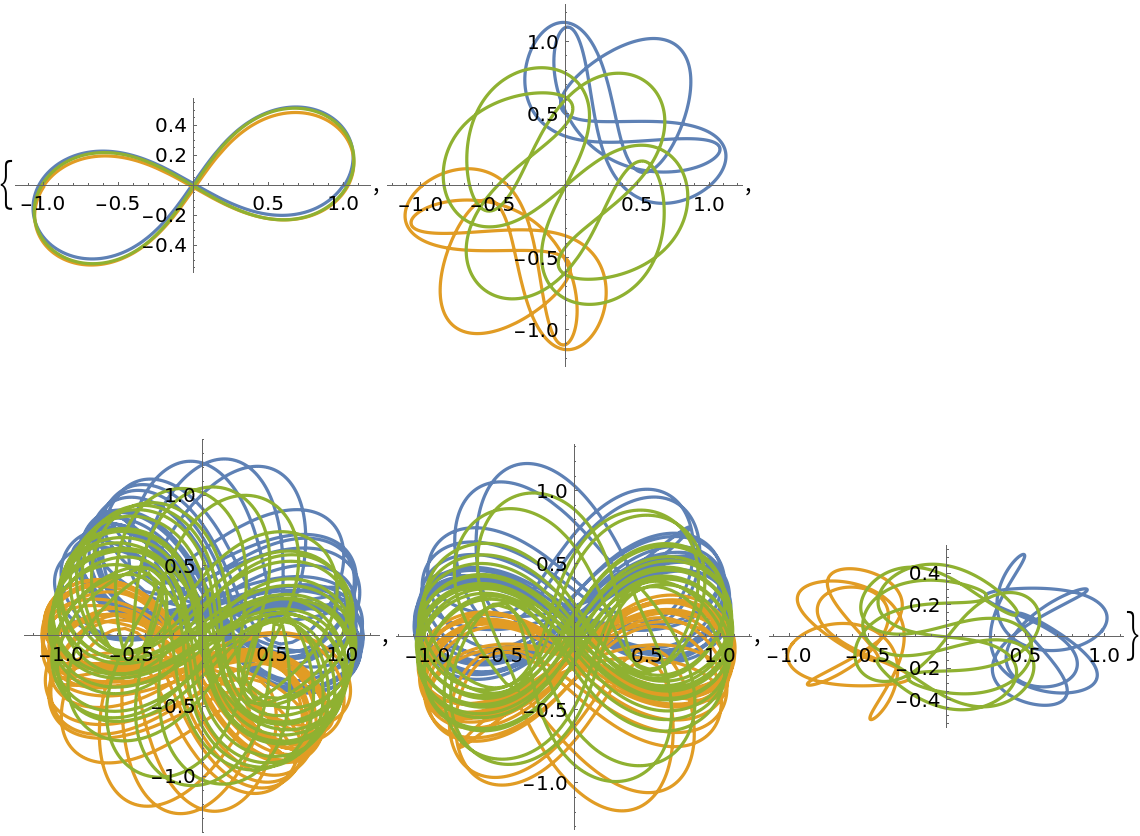

Enrique Zeleny, "Families of Newtonian Periodic Planar Three-Body Orbits" from the Wolfram Data Repository (2022)  

Data Resource History

  • Date Created:

Source Metadata

  • Source: http://numericaltank.sjtu.edu.cn/three-body/three-body-movies.htm
  • Citation:
    • X. Li and S. Liao, "More than six hundreds new families of Newtonian periodic planar collisionless three-body orbits," Sci. China-Phys. Mech. Astron. 60, 129511, 2017. arXiv:1705.00527v4

Data Downloads

Publisher Information

  • Prepared for the Wolfram Data Repository By: Enrique Zeleny
  • Publisher of Record: Enrique Zeleny