Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

GDB-9 Database

Source Notebook

Database of molecular quantum calculations

Details

Computed geometric, energetic, electronic, and thermodynamic properties for 134k stable small organic molecules made up of carbon, hydrogen, nitrogen, oxygen, and fluorine.

Examples

Basic Examples (2) 

Retrieve and load the entity store:

In[1]:=
EntityRegister[ResourceData[\!\(\* TagBox["\"\<GDB-9 Database\>\"", #& , BoxID -> "ResourceTag-GDB-9 Database-Input", AutoDelete->True]\)]];

Find out the number of molecules in the set:

In[2]:=
EntityValue["GDB9Chemical", "EntityCount"]
Out[2]=

Find out the available properties:

In[3]:=
EntityProperties["GDB9Chemical"]
Out[3]=

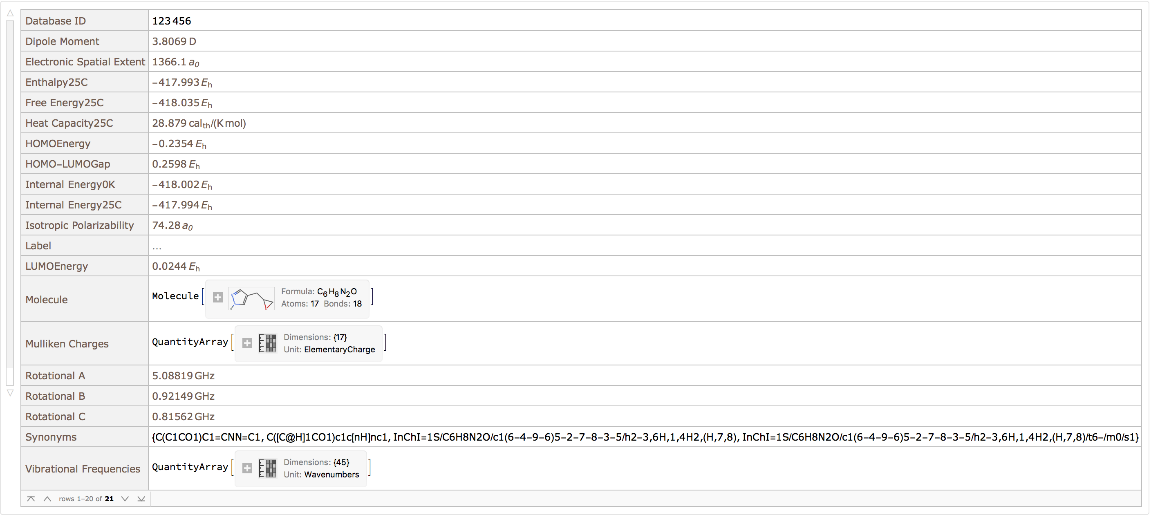
View all property values for a single entity:

In[4]:=
Entity["GDB9Chemical", "GDB123456"]
Out[4]=
In[5]:=
%["Dataset"]
Out[5]=

Query for the Molecule from an entity:

In[6]:=
mol = EntityValue[Entity["GDB9Chemical", "GDB800"], "Molecule"]
Out[6]=
In[7]:=
MoleculePlot3D[mol]
Out[7]=

Scope & Additional Elements (2) 

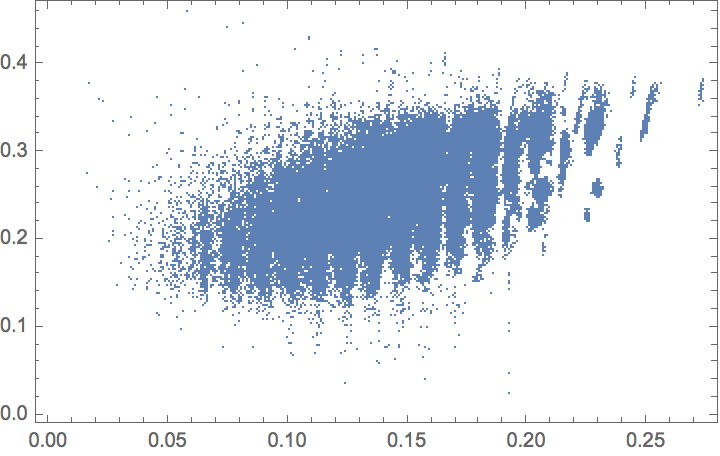
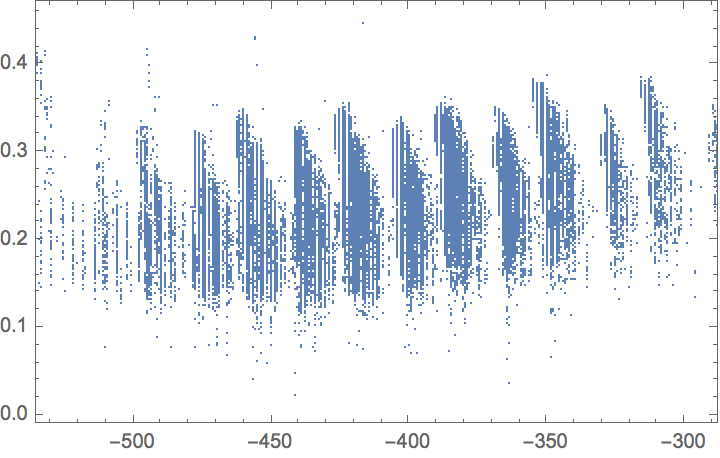
Properties included in the original dataset are available via EntityValue. Make a scatter plot comparing the internal energy calculated at absolute zero versus the HOMO-LUMO gap:

In[8]:=
ListPlot[ EntityValue[ "GDB9Chemical", {EntityProperty["GDB9Chemical", "InternalEnergy0K"], EntityProperty["GDB9Chemical", "HOMO-LUMOGap"]}], Frame -> True]
Out[8]=

Compare the zero-point energy with the HOMO-LUMO gap:

In[9]:=
ListPlot[ EntityValue[ "GDB9Chemical", {EntityProperty["GDB9Chemical", "ZeroPointVibrationalEnergy"], EntityProperty["GDB9Chemical", "HOMO-LUMOGap"]}], Frame -> True]
Out[9]=

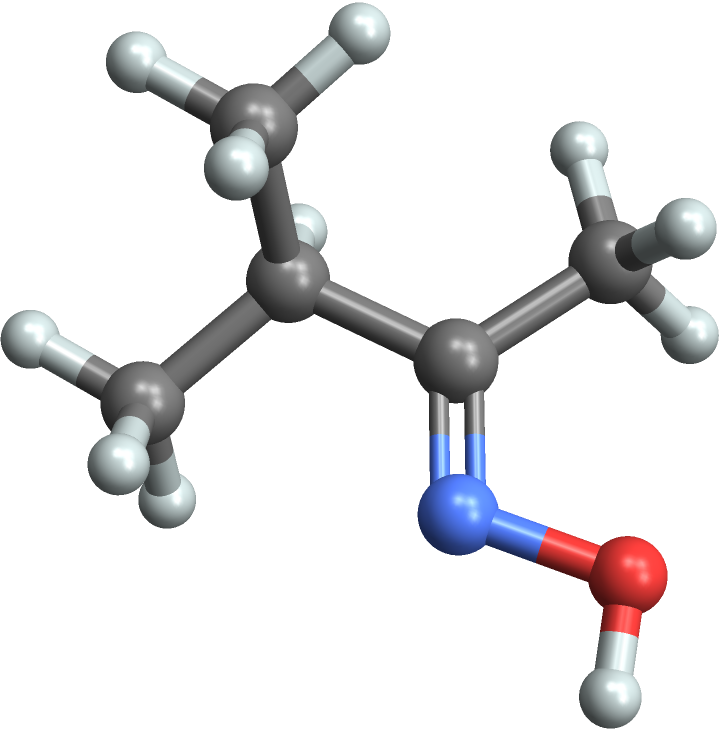
You can compute many more properties than were in the original dataset by creating a Molecule. First take a random entity:

In[10]:=
RandomEntity["GDB9Chemical"]
Out[10]=

Now get the "Molecule" property:

In[11]:=
mol = %["Molecule"]
Out[11]=

Use MoleculeValue to compute properties from the chemical structure:

In[12]:=
MoleculeValue[mol, {"RingCount", "SaturatedRingCount", "RadiusOfGyration", "AdjacencyMatrix"}]
Out[12]=

Visualizations (2) 

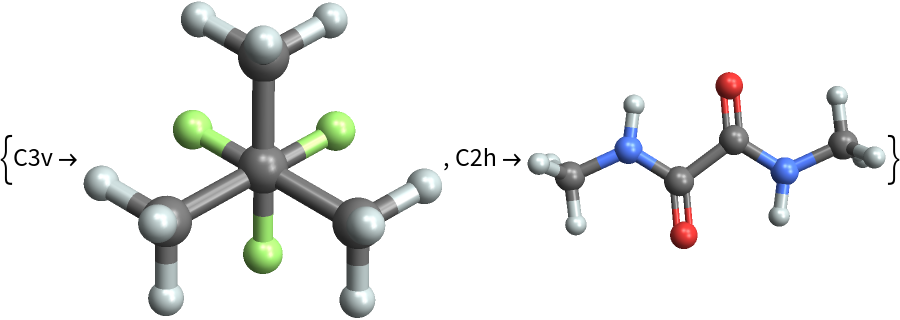
Choose a random set of entities and find those with higher symmetry:

In[13]:=
molecules = EntityValue[RandomEntity["GDB9Chemical", 1000], "Molecule"];
In[14]:=
symm = Select[molecules, ! StringMatchQ[#["PointGroup"], "C" ~~ _] &];
In[15]:=
Length@symm
Out[15]=
In[16]:=
#["PointGroup"] -> MoleculePlot3D[#] & /@ symm
Out[16]=

Analysis (4) 

In this example we find the entities with the most rings. First grab all the molecules from the dataset. Use the "DynamicMap" resource function since this operation takes some time:

In[17]:=
molecules = ResourceFunction["DynamicMap"][ EntityProperty["GDB9Chemical", "Molecule"], EntityList["GDB9Chemical"]];

Find the distribution of ring counts:

In[18]:=
Counts[MoleculeValue[molecules, "RingCount"]]
Out[18]=

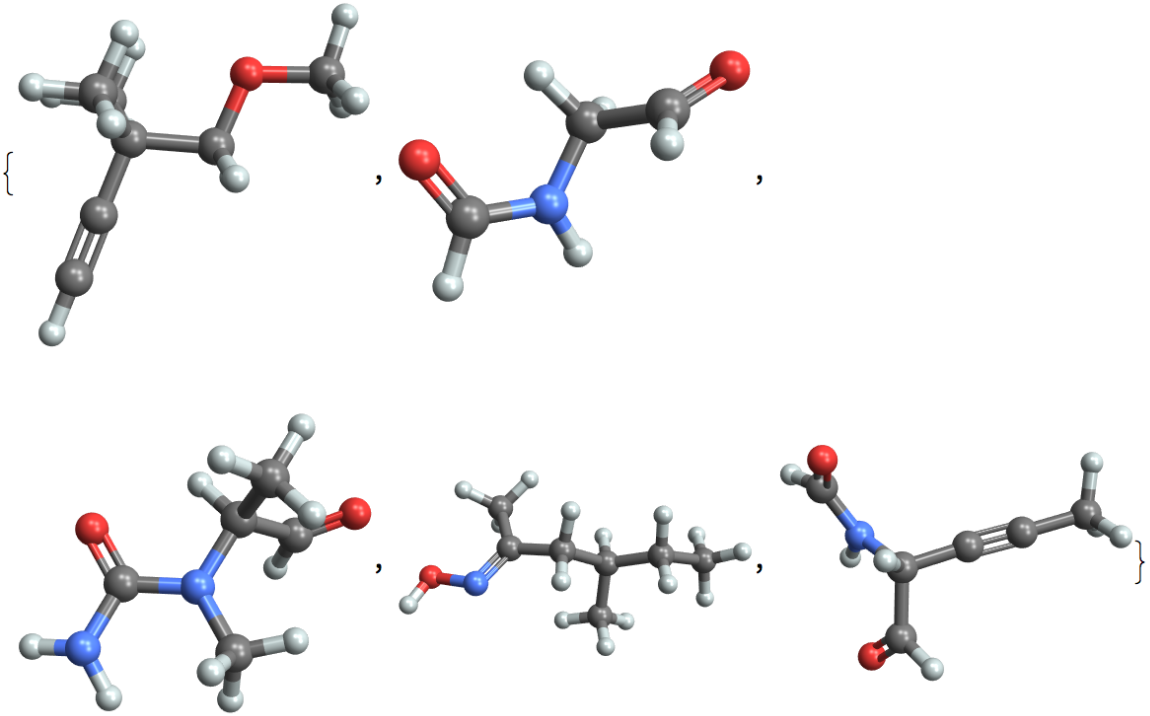
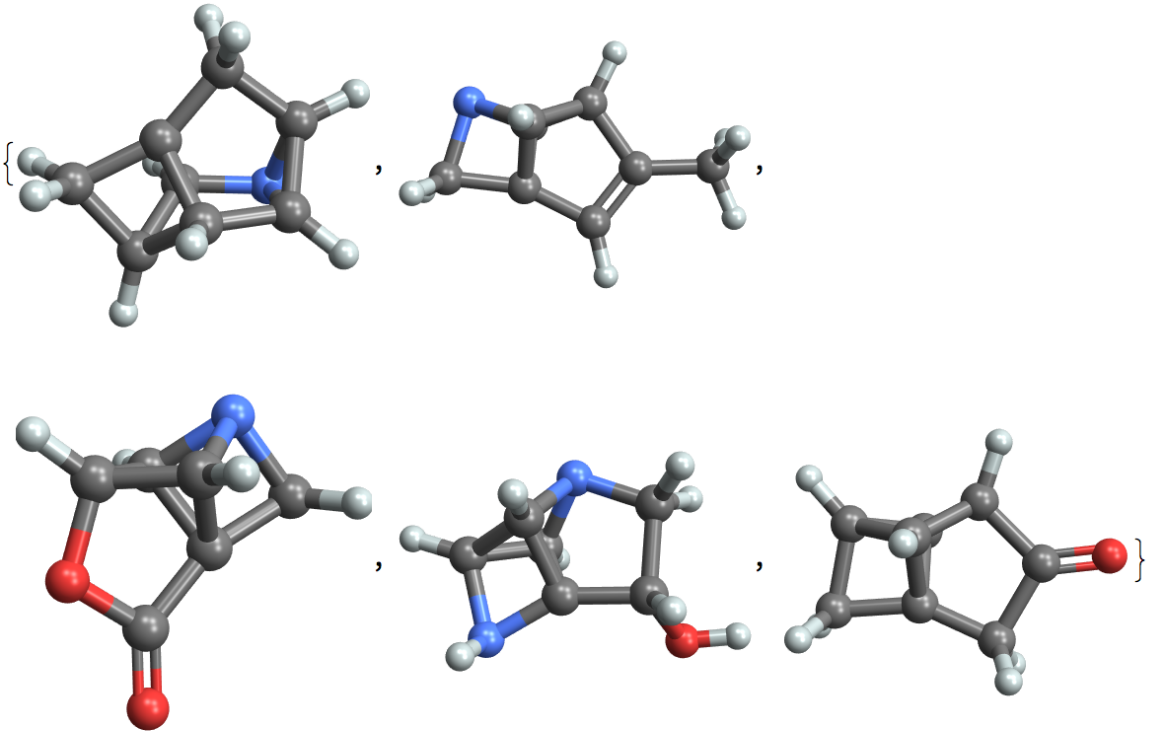
Make 3D plots of some of the acyclic molecules:

In[19]:=
MoleculePlot3D /@ RandomSample[Select[molecules, #["RingCount"] === 0 &], 5]
Out[19]=

Visualize molecules with high ring counts:

In[20]:=
MoleculePlot3D /@ RandomSample[Select[molecules, #["RingCount"] > 6 &], 5]
Out[20]=

Wolfram Research, "GDB-9 Database" from the Wolfram Data Repository (2021)   https://doi.org/10.24097/wolfram.99752.data

License Information

CC0 waiver
http://www.nature.com/sdata/

Data Resource History

  • Date Created:

Source Metadata

  • Title: Quantum chemistry structures and properties of 134 kilo molecules
  • Creator: Raghunathan Ramakrishnan, Pavlo O. Dral, Matthias Rupp, O. Anatole von Lilienfeld
  • Publisher: Nature
  • Date: 5 August 2014
  • Citation:
    • Ramakrishnan, R., Dral, P., Rupp, M. et al. Quantum chemistry structures and properties of 134 kilo molecules. Sci Data 1, 140022 (2014). https://doi.org/10.1038/sdata.2014.22
    • Ramakrishnan, R., Dral, P. O., Rupp, M., & von lilienfeld, O. A. Figshare http://dx.doi.org/10.6084/m9.figshare.978904 (2014)

See Also

Publisher Information

  • Prepared for the Wolfram Data Repository By: Wolfram Research
  • Publisher of Record: Wolfram Research