Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Galton Parent and Child Height Data

Source Notebook

Height of father and mother, child gender and child height as adult for 205 families

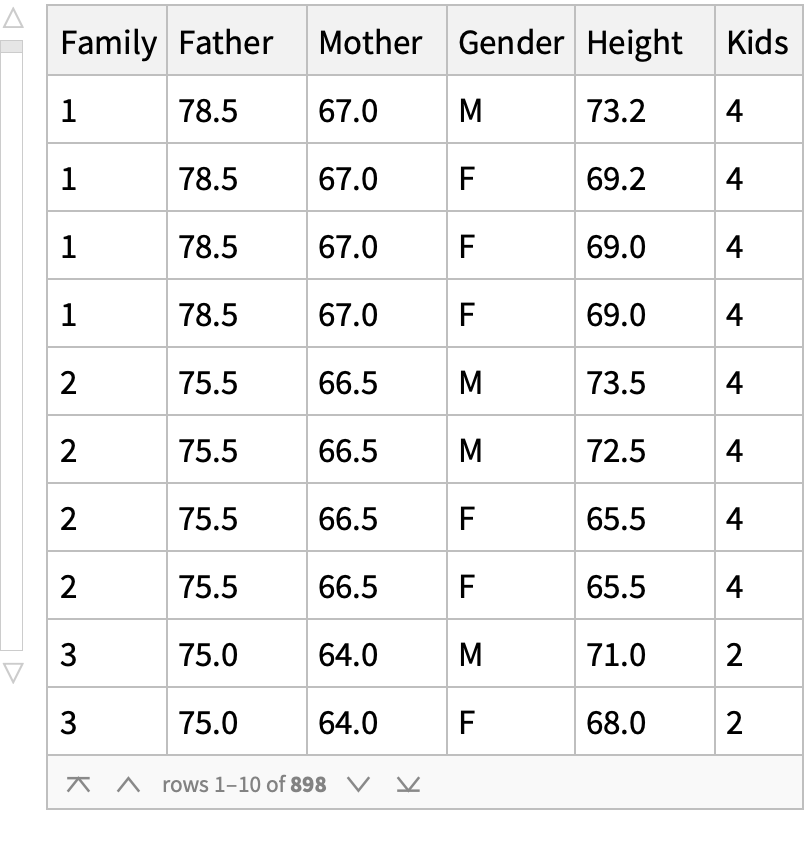
Details

The data are due to Sir Francis Galton. The data set includes the following data for 205 families: The family that the child belongs to numbered from 1 to 205. The height of the father in inches. The height of the mother in inches. The gender of the child with male (M) or female (F). The height of the child in inches. The number of children in family of the child.
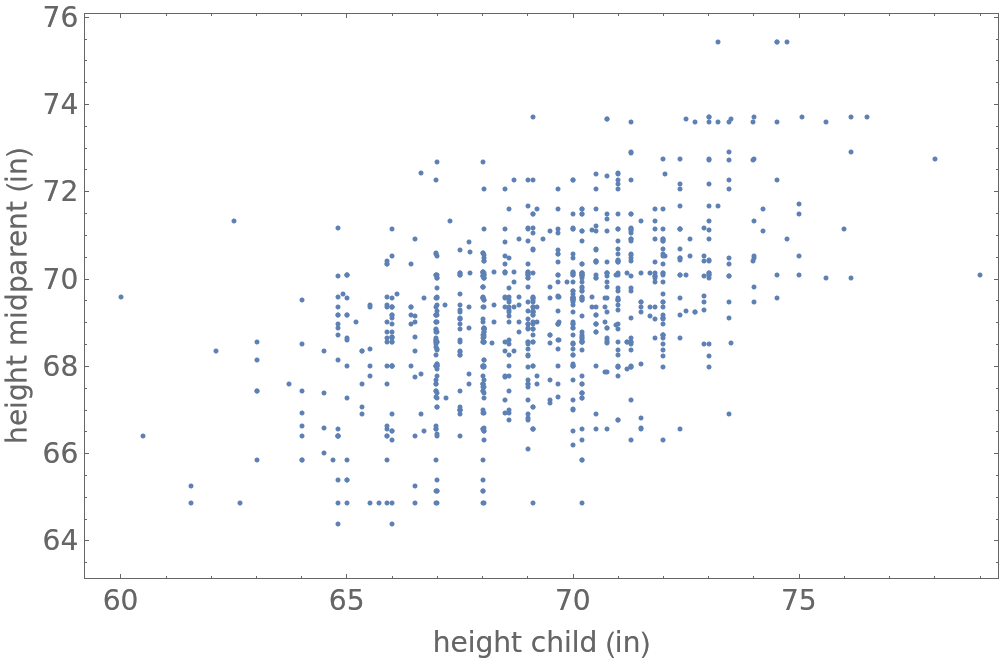
Galton reduced the analysis of the data to two variables by multiplying the female heights of the children by 1.08 and defining what he referred to as a midparent. The height of the midparent was defined to be hmid=(hfather+1.08hmother)/2. That is the midparent height is the average of the father's height and the mother's height adjusted by the factor 1.08. He then considered the distribution of the paired data (hi,ci) where hi is the height of the midparent and ci is the height of the adult child. He found that these data follow a binormal distribution with parameters {μc,μm,σc,σm,ρ) where μ denotes mean, σ denotes standard deviation and ρ is correlation coefficient. The probability density function of the joint distribution of child and midparent height is  log p(h,c)∝(h-μh)2/σh2+(c-μc)2/σc2-2ρ(h-μh)(c-μc)/(σmσc). Thus the distribution is elliptical in shape with the tilt of the ellipse controlled by the correlation ρ.
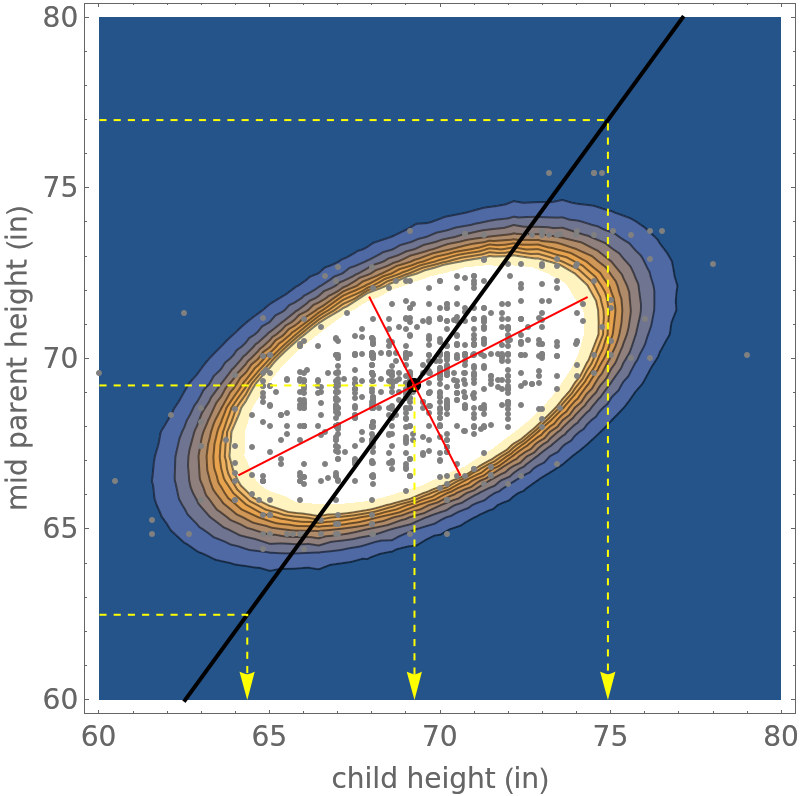
Galton went on to investigate whether children of tall parents tend to be tall and what to degree. He found that children of tall parents tend to be taller than average but not as tall as their parents. Similarly children of shorter parents tend to be shorter than average but taller than their parents. This is referred to as regression to the mean and is necessary in order to maintain a stable distribution of population height.
The mean of the conditional distribution p(c|h=h0) is μc+(h0-μm)ρ σc/σm. If the midparent height in question h0 is equal to the mean of the midparent heights μm then the height of the child can be expect to equal to the mean μc of the children heights. However if the value of h0 is smaller than μm then the height of the child can be expected to be greater than the height of the midparent, but less than average in height. Correspondingly if the value of h0 is greater than μm then the height of the child can be expected to be less than the height of the midparent, but above average in height.

Examples

Basic Examples (4) 

In[1]:=
resource = ResourceData[\!\(\* TagBox["\"\<Galton Parent and Child Height Data\>\"", #& , BoxID -> "ResourceTag-Galton Parent and Child Height Data-Input", AutoDelete->True]\)]
Out[1]=

Compute the mean, standard deviation, and number of samples for the father, mother, male adult child and female adult child data. Note that all heights of children were measured when they were adults. The ratio of the mean height of fathers to the mean height of mothers is 1.08. The ratio of the mean height of male adult children to the mean height of female adult children is also 1.08:

In[2]:=
father = Normal[resource[All, 2]]; mother = Normal[resource[All, 3]]; children = Transpose[Table[Normal[resource[All, i]], {i, {4, 5}}]]; maleAdultChild = Map[Last, Select[children, First[#] == "M" &]]; femaleAdultChild = Map[Last, Select[children, First[#] == "F" &]]; people = {father, mother, maleAdultChild, femaleAdultChild}; mean = Map[Mean, people]; sd = Map[StandardDeviation, people]; ns = Map[Length, people]; type = {"Father", "Mother", "Male child", "Female child"}; TableForm[Transpose[{mean, sd, ns}], TableHeadings -> {type, {"Mean", "Standard deviation", "Samples"}}]
Out[9]=

The following plot indicates that the height of fathers and mothers are normally distributed. The solid lines are the analytical versions of the cumulative distribution function (cdf) for a Gaussian random variable with mean μ and standard deviation σ using the appropriate values for father or mother. The points are the actual observed empirical cdf:

In[10]:=
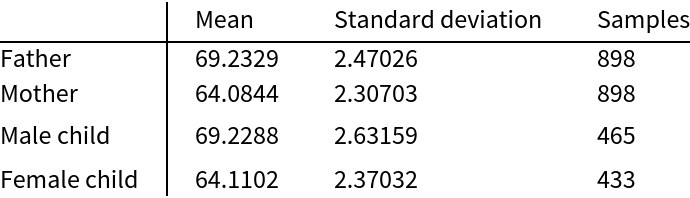
father = Normal[resource[All, 2]]; mother = Normal[resource[All, 3]]; \[Mu]F = Mean[father]; sF = StandardDeviation[father]; nF = Length[father]; \[Mu]M = Mean[mother]; sM = StandardDeviation[mother]; nM = Length[mother]; cdfF = Transpose[{Sort[father], Table[i/(nF + 1), {i, 1, nF}]}]; cdfM = Transpose[{Sort[mother], Table[i/(nM + 1), {i, 1, nM}]}]; min = Min[mother]; max = Max[father]; Plot[{CDF[NormalDistribution[\[Mu]F, sF], h], CDF[NormalDistribution[\[Mu]M, sM], h]}, {h, min, max}, Epilog -> {{Gray, Point[cdfF]}, {Opacity[0.3], Gray, Point[cdfM]}}, Sequence[ AxesLabel -> {"in", "CDF"}, PlotStyle -> {Thick, Thick}, PlotLegends -> {"father", "mother"}]]
Out[16]=

The following plot indicates that the heights of the male and female adult children are each normally distributed. The solid lines are the analytical versions of the cumulative distribution function (cdf) for a Gaussian random variable with mean μ and standard deviation σ using the appropriate values for male or female adult child. The points are the actual observed empirical cdf:

In[17]:=
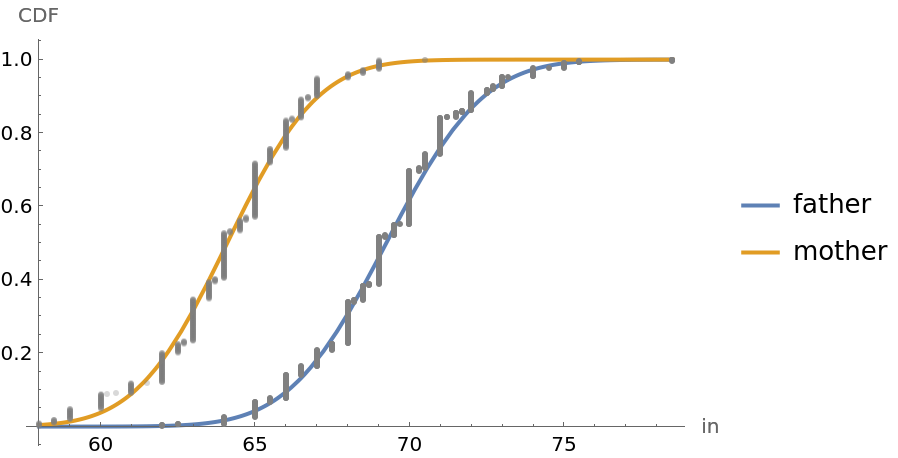
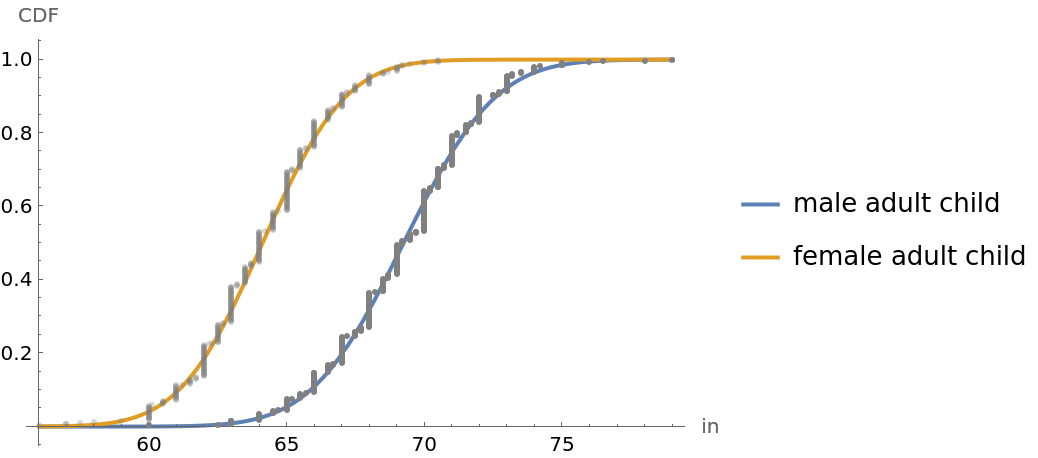
children = Transpose[Table[Normal[resource[All, i]], {i, {4, 5}}]]; mC = Map[Last, Select[children, First[#] == "M" &]]; fC = Map[Last, Select[children, First[#] == "F" &]]; \[Mu]mC = Mean[mC]; smC = StandardDeviation[mC]; nmC = Length[mC]; \[Mu]fC = Mean[fC]; sfC = StandardDeviation[fC]; nfC = Length[fC]; cdfmC = Transpose[{Sort[mC], Table[i/(nmC + 1), {i, 1, nmC}]}]; cdffC = Transpose[{Sort[fC], Table[i/(nfC + 1), {i, 1, nfC}]}]; min = Min[fC]; max = Max[mC]; Plot[{CDF[NormalDistribution[\[Mu]mC, smC], h], CDF[NormalDistribution[\[Mu]fC, sfC], h]}, {h, min, max}, Epilog -> {{Gray, Point[cdfmC]}, {Opacity[0.3], Gray, Point[cdffC]}}, Sequence[ AxesLabel -> {"in", "CDF"}, PlotStyle -> {Thick, Thick}, PlotLegends -> {"male adult child", "female adult child"}]]
Out[25]=

Test the heights of fathers for normality using a variety of tests. Small p-values indicate that the data are normally distributed:

In[26]:=
\[ScriptCapitalH] = DistributionFitTest[father, Automatic, "HypothesisTestData"]; \[ScriptCapitalH]["TestDataTable", All]
Out[27]=

Visualizations (2) 

Retrieve the data and parse through the data organizing the results as pairs of (child height, midparent height). Then plot a scatter plot of the results. The data are obviously correlated:

In[28]:=
resource = ResourceData[\!\(\* TagBox["\"\<Galton Parent and Child Height Data\>\"", #& , BoxID -> "ResourceTag-Galton Parent and Child Height Data-Input", AutoDelete->True]\)]; data = Table[ {f, m, g, h} = {"Father", "Mother", "Gender", "Height"} /. Normal[resource[[i]]]; mid = (f + 1.08 m)/2; {If[g == "M", h, 1.08 h], mid}, {i, 1, Length[resource]}]; ListPlot[data, Sequence[ PlotRange -> All, Axes -> False, Frame -> True, PlotRange -> All, FrameLabel -> {"height child (in)", "height midparent (in)"}, ImageSize -> 500, BaseStyle -> {FontSize -> 14}]]
Out[29]=

Visually compare heights of children to heights of midparents and observe that there is more spread in the heights of children than parents:

In[30]:=
{child, midparent} = Transpose[data]; Clear[a, b]; edc = EstimatedDistribution[child, NormalDistribution[a, b]]; edm = EstimatedDistribution[midparent, NormalDistribution[a, b]]; gc = Show[ Histogram[child, {60, 80, 1}, "PDF", PlotLabel -> "child", AxesLabel -> {"in"}], Plot[PDF[edc, x], {x, 60, 80}]]; gm = Show[ Histogram[midparent, {60, 80, 1}, "PDF", Sequence[ PlotLabel -> "midparent", AxesLabel -> {"in"}]], Plot[PDF[edm, x], {x, 60, 80}]]; GraphicsRow[{gm, gc}]
Out[31]=

Analysis (2) 

Fit the midparent-child data to a binormal distribution and display the parameters of the fit:

In[32]:=
resource = ResourceData[\!\(\* TagBox["\"\<Galton Parent and Child Height Data\>\"", #& , BoxID -> "ResourceTag-Galton Parent and Child Height Data-Input", AutoDelete->True]\)]; data = Table[ {f, m, g, h} = {"Father", "Mother", "Gender", "Height"} /. Normal[resource[[i]]]; mid = (f + 1.08 m)/2; {If[g == "M", h, 1.08 h], mid}, {i, 1, Length[resource]}]; Clear[\[Mu]c, \[Mu]m, \[Sigma]c, \[Sigma]m, \[Rho], x, y, y0]; dist = EstimatedDistribution[data, BinormalDistribution[{\[Mu]c, \[Mu]m}, {\[Sigma]c, \[Sigma]m}, \[Rho]]]; {\[Mu]c, \[Mu]m} = dist[[1]]; {\[Sigma]c, \[Sigma]m} = dist[[2]]; \[Rho] = dist[[3]]; TableForm[{{\[Mu]c, \[Mu]m, \[Sigma]c, \[Sigma]m, \[Rho]}}, TableHeadings -> {None, {"\[Mu]c", "\[Mu]m", "\[Sigma]c", "\[Sigma]m", "\[Rho]"}}]
Out[33]=

The following plot compares the analytical cumulative distribution of the fit to the observed data. The red lines indicate the major and minor axes of the fitted binormal distribution. The thick black line indicates the conditional mean of child height given a specific midparent height. The dashed yellow lines indicate the phenomena of convergence to the mean that Galton identified in his work. For instance, a midparent of height 77 in produces on average a child of height 75 in. The average child is taller than average but less than the height of the midparent. A midparent of height 62.5 in produces on average a child of height 64.5 in. This average child is taller than the height of the midparent but less than average in height. The midparent of average height (see center group of dashed yellow line and large black dot in figure) produces a child of average height, both averages being equal:

In[34]:=
xmin = 60; xmax = 80; ymin = 60; ymax = 80; mean = {PointSize[0.02], Point[{\[Mu]c, \[Mu]m}]}; datapoints = {Gray, Point[data]}; reference = Table[pnt1 = {xmin, y0}; pnt2 = {\[Mu]c + ((y0 - \[Mu]m) \[Rho] \[Sigma]c)/\[Sigma]m, y0}; pnt3 = {\[Mu]c + ((y0 - \[Mu]m) \[Rho] \[Sigma]c)/\[Sigma]m, ymin}; ref = {Yellow, Dashing[0.01], Arrow[{pnt1, pnt2, pnt3}]}; ref, {y0, {62.5, \[Mu]m, 77}}]; conditional = {Black, Thick, Line[Table[{\[Mu]c + ((y0 - \[Mu]m) \[Rho] \[Sigma]c)/\[Sigma]m, y0}, {y0, ymin, ymax, 0.1}]]}; major = {Red, Line[Table[{\[Mu]c + (y0 - \[Mu]m)/\[Rho], y0}, {y0, 66.6, 71.85, 0.1}]]}; minor = {Red, Line[Table[{\[Mu]c - \[Rho] (y0 - \[Mu]m), y0}, {y0, 66.6, 71.85, 0.1}]]}; ContourPlot[PDF[dist, {x, y}], {x, xmin, xmax}, {y, ymin, ymax}, Epilog -> {datapoints, mean, conditional, reference, major, minor}, Sequence[ AspectRatio -> 1, FrameLabel -> {"child height (in)", "mid parent height (in)"}, ImageSize -> 400, BaseStyle -> {FontSize -> 14}]]
Out[35]=

Marshall Bradley, "Galton Parent and Child Height Data" from the Wolfram Data Repository (2022)  

Data Resource History

  • Date Created:

Data Downloads

Publisher Information

  • Prepared for the Wolfram Data Repository By: Marshall Bradley
  • Publisher of Record: Marshall Bradley