Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Gliders in 2D Cellular Automata

A 2D cellular automaton glider compilation by David Eppstein

Originator: David Eppstein

(21690 elements)

Examples

Basic Examples

Show a glider with a very long period:

In[1]:=
ResourceData["Gliders in 2D Cellular Automata"][13047]
Out[1]=

Show gliders that work in rule 224, the Game of Life:

In[2]:=
With[{data = ResourceData["Gliders in 2D Cellular Automata"]}, Grid[Partition[Row[ {Column[ If[Head[#] === Missing, Sequence @@ {}, #] & /@ {Row[{"index ", #}], data[[#]]["GliderName"], data[[#]]["DiscoveryNotes"], Row[{"period ", data[[#]]["Period"]}], Row[{"displacement ", data[[#]]["Displacement"]}], Row[{"size ", data[[#]]["MinimumSize"]}]}], ArrayPlot[data[[#]]["GliderArray"], ImageSize -> {120, 120}]}] & /@ Take[{115, 1062, 9153, 10240, 11302, 13374, 13491, 13881, 14105, 16485, 16532, 17361, 18216, 18788, 19739, 21362}, 15], 3]]]
Out[2]=

Show the index, displacement, and initial state of gliders that do not move orthogonally or diagonally, AKA the knight-gliders since they can move like a chess knight:

In[3]:=
With[{data = ResourceData["Gliders in 2D Cellular Automata"]}, Grid[Partition[ Framed[Text@Column[#[[2]], Alignment -> Center]] & /@ Normal[{#["DatabaseIndex"], #["Displacement"], ArrayPlot[#["GliderArray"], ImageSize -> {60, 60}, Frame -> False]} & /@ SortBy[Select[ data, #["Displacement"][[1]] > #["Displacement"][[2]] > 0 && #["Period"] < 50 &], Max[#[["MinimumSize"]]] &]], 11]]]
Out[3]=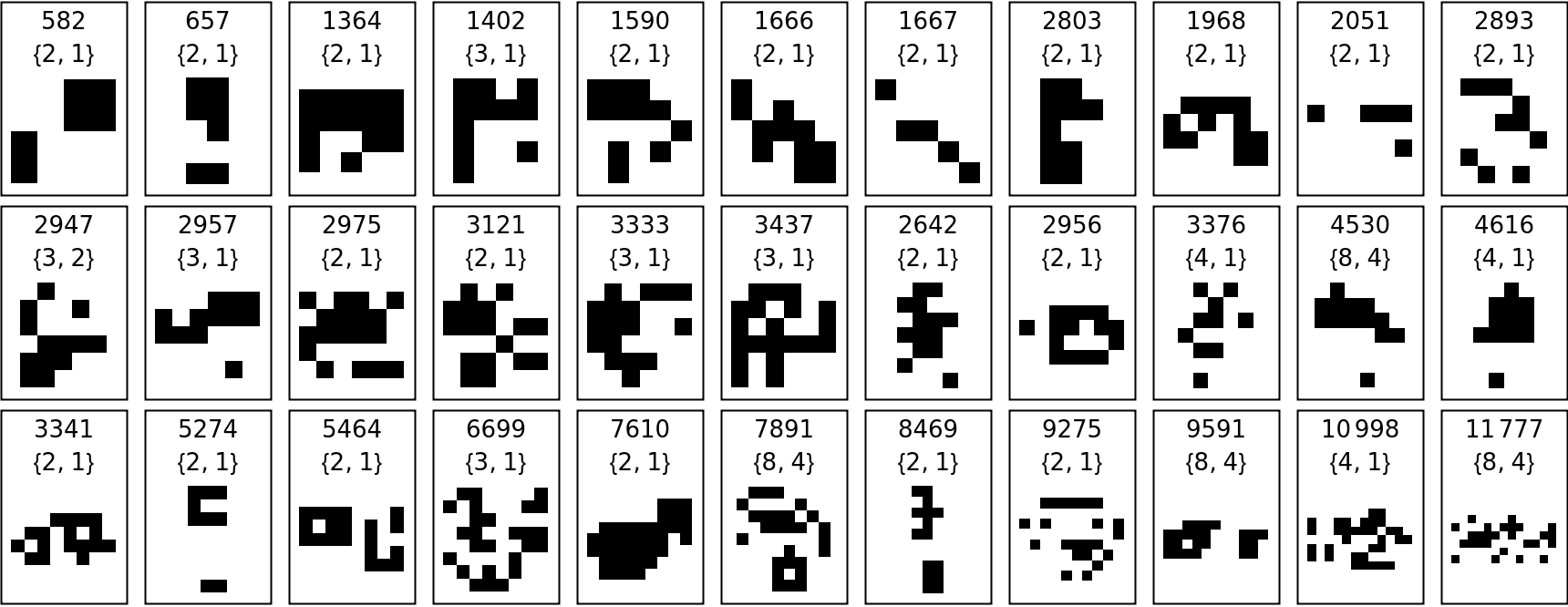

Wolfram Research, "Gliders in 2D Cellular Automata" from the Wolfram Data Repository (2017)   https://doi.org/10.24097/wolfram.01559.data

Data Resource History

  • Date Created:

Source Metadata

  • Source: http://fano.ics.uci.edu/glider.db
  • Citation: Glider Database

Data Downloads

Publisher Information

  • Prepared for the Wolfram Data Repository By: Ed Pegg Jr
  • Publisher of Record: Wolfram Research