Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

H(6,4) Hamming Graph

The Second DIMACS Implementation Challenge: 1992-1993

Originator: Panos Pardalos

NP Hard Problems: Maximum Clique, Graph Coloring, and Satisfiability, The Second DIMACS Implementation Challenge: 1992-1993.

A Hamming graph with parameters n and d has a node for each binary vector of length n. Two nodes are adjacent if and only if the corresponding bit vectors are hamming distance at least d apart.

(64 vertices, 704 edges)

Examples

Basic Examples

Retrieve the graph:

In[1]:=
ResourceData["H(6,4) Hamming Graph"]
Out[1]=

Summary properties:

In[2]:=
ResourceData["H(6,4) Hamming Graph", All]["Summary"]
Out[2]=

Basic Applications

Find the maximum clique:

In[3]:=
g = ResourceData["H(6,4) Hamming Graph"];
In[4]:=
maxclique = FindClique[g]
Out[4]=

Show the maximum clique:

In[5]:=
HighlightGraph[g, Subgraph[g, maxclique], VertexCoordinates -> ReplacePart[ GraphEmbedding[g, "SpringElectricalEmbedding"], Thread[Map[VertexIndex[g, #]& , First[maxclique]] -> CirclePoints[{3., 0.9}, 0.5, Length[ First[maxclique]]]]], Sequence[ EdgeStyle -> {Blank[] -> Opacity[0.05]}, GraphLayout -> "SpringElectricalEmbedding", VertexSize -> {Blank[] -> 0.5}]]
Out[6]=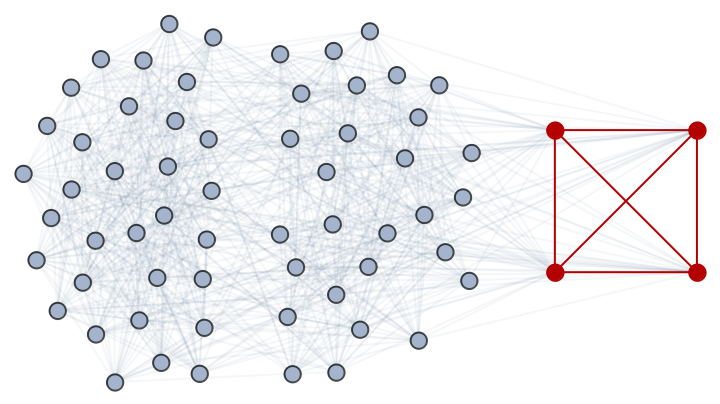

Wolfram Research, "H(6,4) Hamming Graph" from the Wolfram Data Repository (2019)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • Volume 26, Cliques, Coloring, and Satisfiability: Second DIMACS Implementation Challenge, October 11-13, 1993, Editors: David S. Johnson and Michael A. Trick; AMS, Providence, RI, 1996.

Publisher Information

  • Prepared for the Wolfram Data Repository By: Wolfram
  • Publisher of Record: Wolfram Research