Wolfram Research

Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Sample Data: Hamster Tumour

Source Notebook

Locations of cell nuclei in hamster kidney annotated with type

Details

Locations of cell nuclei in hamster kidney in the observation region Rectangle[{0, 0}, {1, 1}]*250 microns, annotated with type.

Examples

Basic Examples (1) 

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Sample Data: Hamster Tumour\>\"", #& , BoxID -> "ResourceTag-Sample Data: Hamster Tumour-Input", AutoDelete->True]\), "Data"]
Out[1]=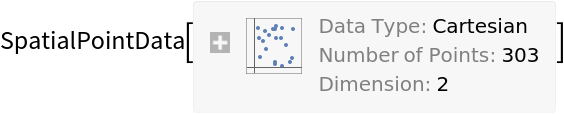

Summary of the spatial point data:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<Sample Data: Hamster Tumour\>\"", #& , BoxID -> "ResourceTag-Sample Data: Hamster Tumour-Input", AutoDelete->True]\), "Data"]["Summary"]
Out[2]=

Visualizations (2) 

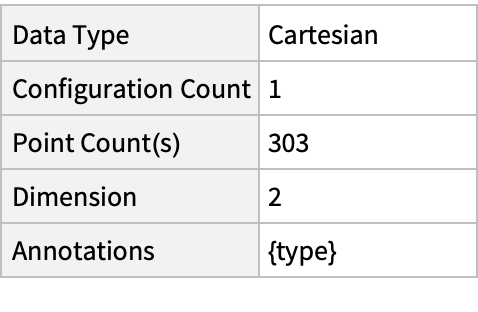Plot the spatial point data:

In[3]:=
ListPlot[ResourceData[\!\(\* TagBox["\"\<Sample Data: Hamster Tumour\>\"", #& , BoxID -> "ResourceTag-Sample Data: Hamster Tumour-Input", AutoDelete->True]\), "Data"], AspectRatio -> 1]
Out[3]=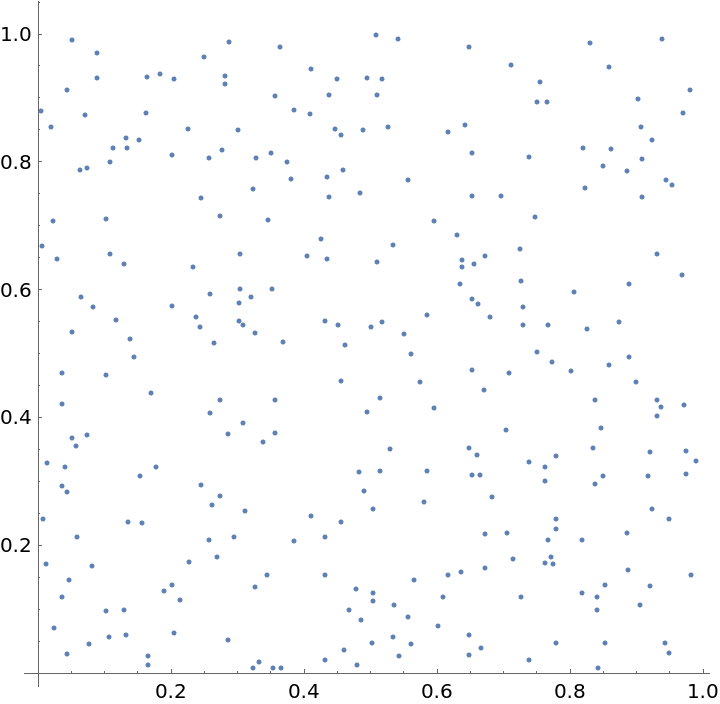

Visualize points with the type annotations:

In[4]:=
PointValuePlot[ResourceData[\!\(\* TagBox["\"\<Sample Data: Hamster Tumour\>\"", #& , BoxID -> "ResourceTag-Sample Data: Hamster Tumour-Input", AutoDelete->True]\), "Data"], PlotLegends -> Automatic]
Out[4]=

Analysis (5) 

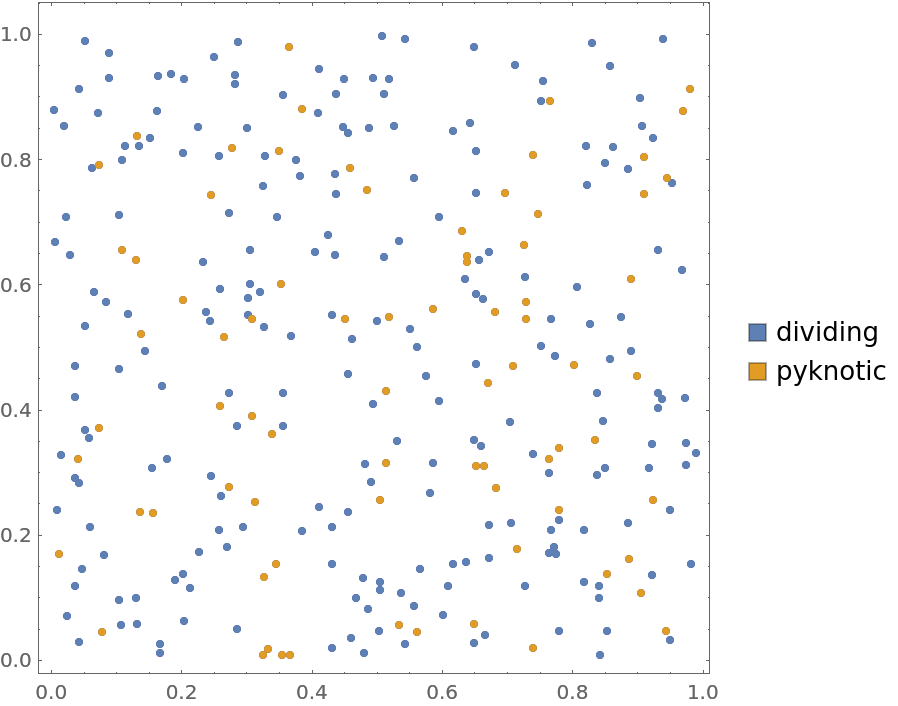Compute probability of finding a point within given radius of an existing point - NearestNeighborG is the CDF of the nearest neighbor distribution:

In[5]:=
nnG = NearestNeighborG[ResourceData[\!\(\* TagBox["\"\<Sample Data: Hamster Tumour\>\"", #& , BoxID -> "ResourceTag-Sample Data: Hamster Tumour-Input", AutoDelete->True]\), "Data"]]
Out[5]=
In[6]:=
maxR = nnG["MaxRadius"]
Out[6]=
In[7]:=
DiscretePlot[nnG[r], {r, maxR/100, maxR, maxR/100}, AxesLabel -> {"radius", "probability"}]
Out[7]=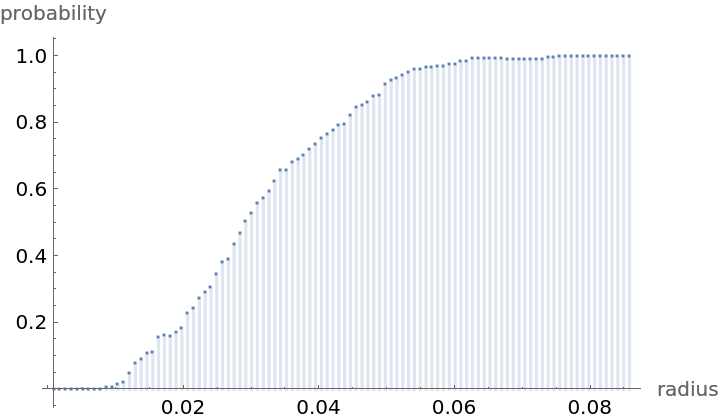

Mean distance between a typical point and its nearest neighbor (for positive support distribution can be approximated via a Riemann sum of 1-CDF):

In[8]:=
step = maxR/100; partition = Table[{k, k + step}, {k, 0, maxR, step}]; values = nnG[Mean /@ partition];
In[9]:=
Total[(1 - values)*step]
Out[9]=

Conform to scale:

In[10]:=
%*ResourceData[\!\(\* TagBox["\"\<Sample Data: Hamster Tumour\>\"", #& , BoxID -> "ResourceTag-Sample Data: Hamster Tumour-Input", AutoDelete->True]\), "RegionScale"]
Out[10]=

Test for complete spacial randomness:

In[11]:=
SpatialRandomnessTest[ResourceData[\!\(\* TagBox["\"\<Sample Data: Hamster Tumour\>\"", #& , BoxID -> "ResourceTag-Sample Data: Hamster Tumour-Input", AutoDelete->True]\), "Data"], {"PValue", "TestConclusion"}]
Out[11]=

Fit a Poisson point process to data:

In[12]:=
EstimatedPointProcess[ResourceData[\!\(\* TagBox["\"\<Sample Data: Hamster Tumour\>\"", #& , BoxID -> "ResourceTag-Sample Data: Hamster Tumour-Input", AutoDelete->True]\), "Data"], PoissonPointProcess[\[Mu], 2]]
Out[12]=

Gosia Konwerska, "Sample Data: Hamster Tumour" from the Wolfram Data Repository (2022)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation: Diggle, P.J. (1983) Statistical analysis of spatial point patterns. Academic Press.

Publisher Information

  • Prepared for the Wolfram Data Repository By: Gosia Konwerska
    (Wolfram Research, Inc.)
  • Publisher of Record: Gosia Konwerska