Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

J(8,2,4) Generalized Johnson Graph

The Second DIMACS Implementation Challenge: 1992-1993

Originator: Panos Pardalos

NP Hard Problems: Maximum Clique, Graph Coloring, and Satisfiability, The Second DIMACS Implementation Challenge: 1992-1993.

A Johnson graph with parameters n, w, d has a node for every binary vector of length n with exactly w 1s. Two vertices are adjacent if and only if their hamming distance is at least d.

(120 vertices, 5460 edges)

Examples

Basic Examples

Retrieve the graph:

In[1]:=
ResourceData["J(8,2,4) Generalized Johnson Graph"]
Out[1]=

Summary properties:

In[2]:=
ResourceData["J(8,2,4) Generalized Johnson Graph", All]["Summary"]
Out[2]=

Basic Applications

Find the maximum clique:

In[3]:=
g = ResourceData["J(8,2,4) Generalized Johnson Graph"];
In[4]:=
maxclique = FindClique[g]
Out[4]=
In[5]:=
maxclique = {{3, 4, 15, 28, 45, 66, 91, 120}};

Show the maximum clique:

In[6]:=
HighlightGraph[g, Subgraph[g, maxclique], VertexCoordinates -> ReplacePart[ GraphEmbedding[g, "SpringElectricalEmbedding"], Thread[Map[VertexIndex[g, #]& , First[maxclique]] -> CirclePoints[{2.6, 0.9}, 0.5, Length[ First[maxclique]]]]], Sequence[ EdgeStyle -> {Blank[] -> Opacity[0.05]}, GraphLayout -> "SpringElectricalEmbedding", VertexSize -> {Blank[] -> 0.5}]]
Out[15]=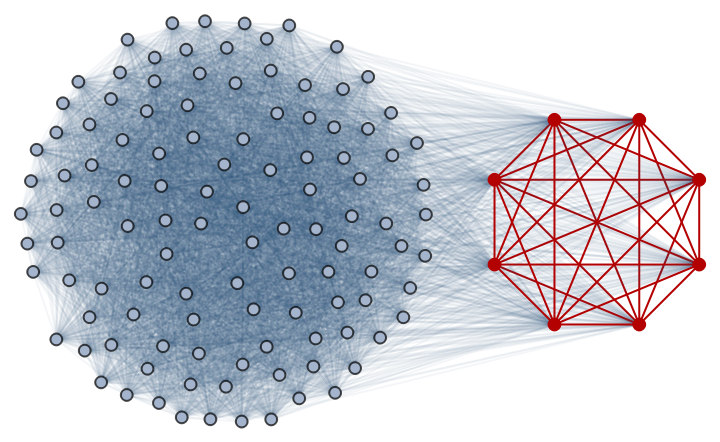

Wolfram Research, "J(8,2,4) Generalized Johnson Graph" from the Wolfram Data Repository (2019)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • Volume 26, Cliques, Coloring, and Satisfiability: Second DIMACS Implementation Challenge, October 11-13, 1993, Editors: David S. Johnson and Michael A. Trick; AMS, Providence, RI, 1996.

Data Downloads

Publisher Information

  • Prepared for the Wolfram Data Repository By: Wolfram
  • Publisher of Record: Wolfram Research