Basic Examples

Retrieve the resource:

In[1]:=

Out[1]=

Retrieve the default content:

In[2]:=

Out[2]=

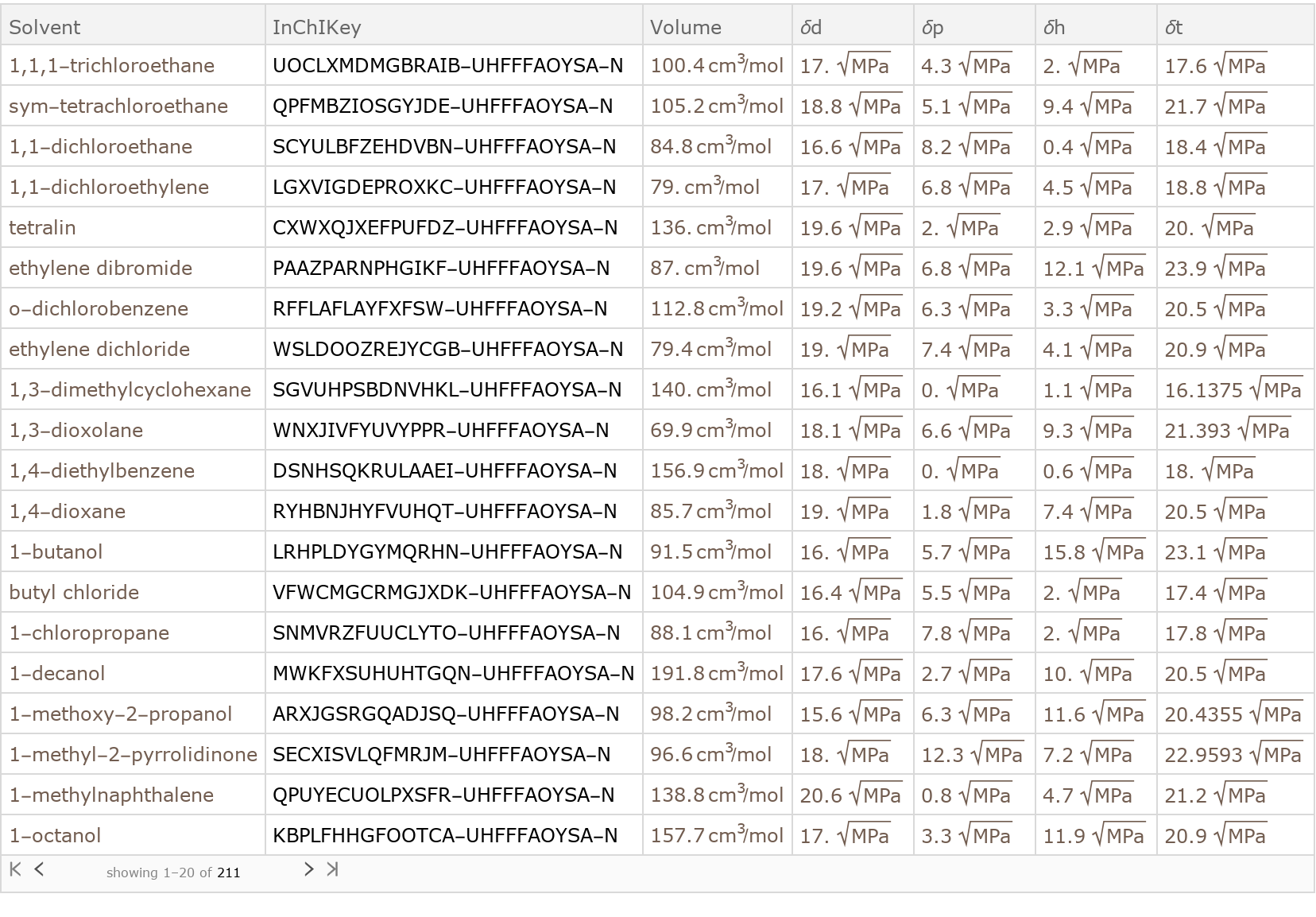
Searching Entries by CAS and Beilstein Index Numbers

Because the Solvent entries are described by Chemical entities, the properties of those entities can be queries to provide access to other indexing schemes, such as the CAS Number of the molecule:

In[3]:=

Out[3]=

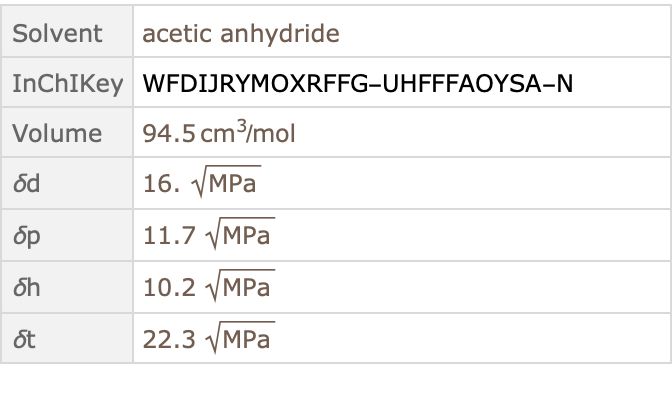
This allows us to construct queries based on these identifiers contained in the Chemical entity, in addition to the InChIKey identifier provided in the data resource:

In[4]:=

Out[4]=

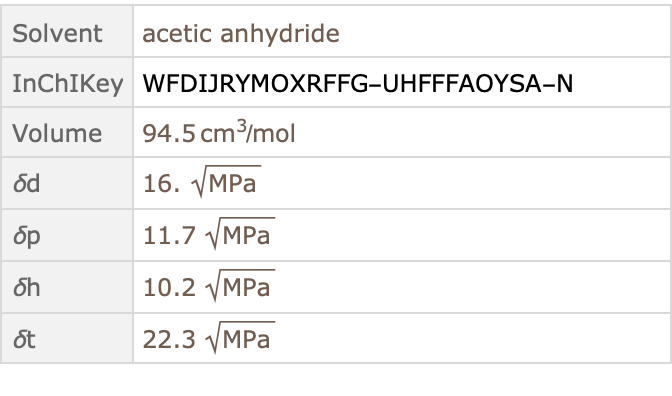
Similarly, Beilstein numbers are contained in the Chemical entity entries. Not all of the Wolfram Chemical Entities have Beilstein number data, so it is useful to define the FailureAction for the Query to ignore these:

In[5]:=

Out[5]=

Creation of Molecule representations:

The Chemical entities contain SMILES and InChI representations of the molecular structure that can be used for constructing Molecule representations:

In[6]:=

Out[6]=

Out[7]=

In[8]:=

Out[8]=

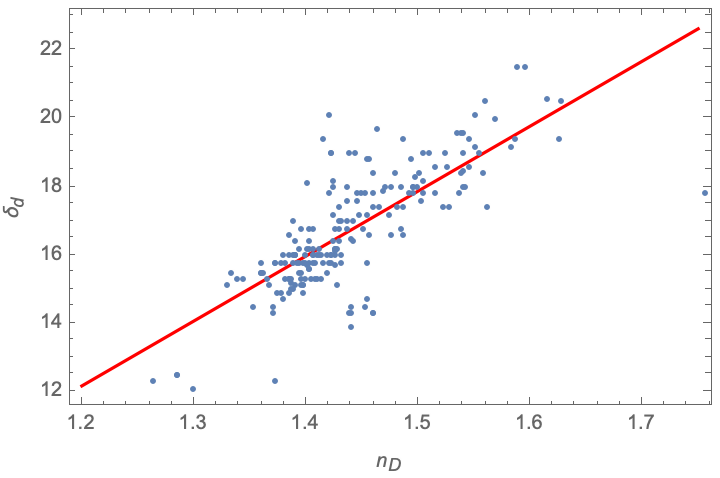
Correlation between dispersive parameter and refractive index

The interaction energy between nonpolar molecules should depend on the molar polarizability (London dispersion forces) and therefore the index of refraction; this is represented by the dispersive parameter, δ_d. Extract these values, deleting entries where the Chemical entity lacks the refractive index data:

In[9]:=

Out[10]=

Out[11]=

Out[12]=

The fitted parameters to this data are about twice the values reported in Eqn 16.19 of Zeng et al.'s paper from which this data was extracted. However, this does appear to be the correct fit for the dataset:

In[13]:=

Out[13]=

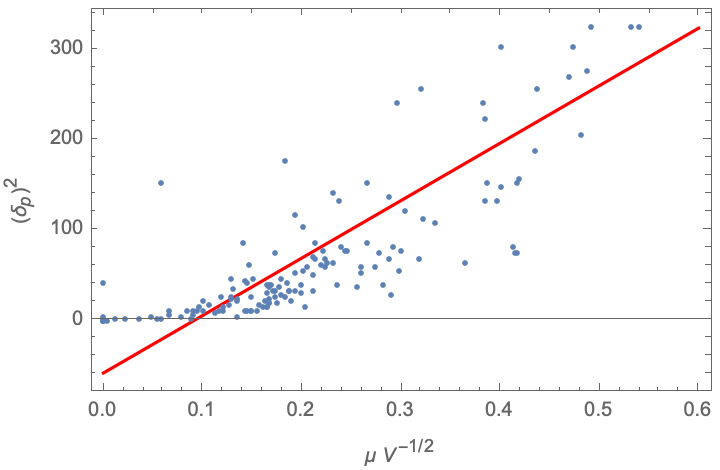
Correlation between dipole moment, volume, and polar parameter

Zeng et al. note an empirical relationship observed by Beerbower and Dicky (1969) between the dipole moment, molar volume, and the polar parameter, δ_p. Again we can extract the dipole moment from the Chemical entity, using the molar volume provided in the dataset as the "Volume" column:

In[14]:=

Out[15]=

Out[16]=

Out[17]=

A Plot of the fit shows the general trend, although there are number of examples for which the polar parameter is set to zero for very weakly polar molecules:

In[18]:=

Out[18]=

Finding compatible solvents

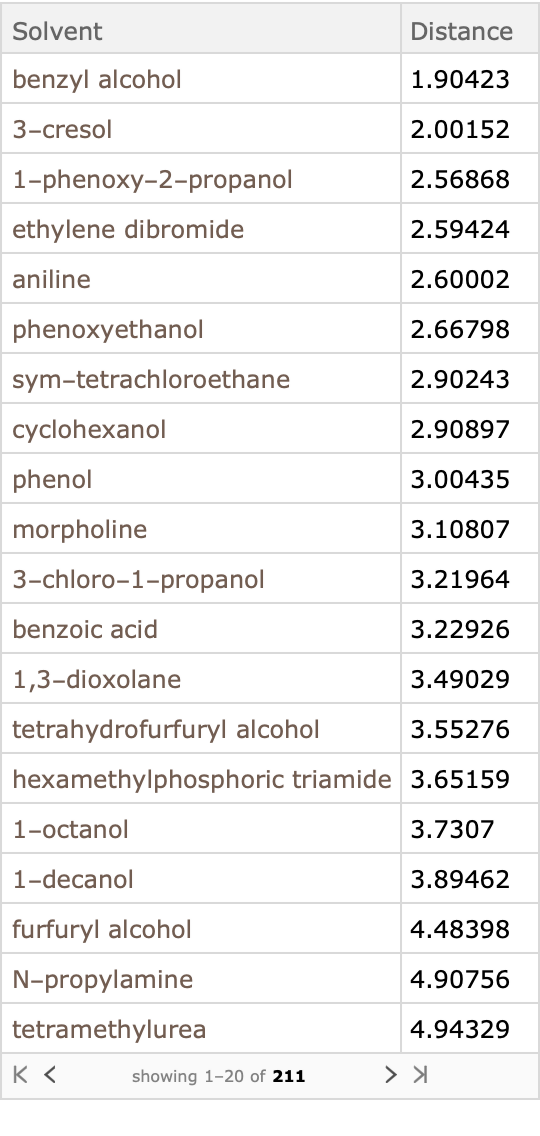
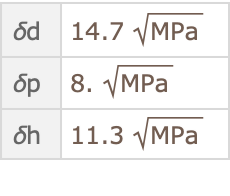
Hansen parameters quantify “like dissolves like” solvation rules by the distance between a solutes Hansen triple (usually empirically determined), and the solvent properties. There is a modified Euclidean distance between the solute and solvent triples (the dispersive feature, δd, has an additional factor of 4). For example, a particular formulation of Nylon-66 has the Hanson triple:

In[19]:=

Construct a query to compute the distance:

In[20]:=

Apply this query to the dataset, sorting by Distance; the solvents with the smallest distance are predicted to be better solvents:

In[21]:=

Out[21]=

Empirically, Nylon-66 is soluble in phenolic alcohols (such as cresol, and phenol), and poor resistance to tetrachlorethane (correctly described by the Hanson model), moderate resistance to benzyl alcohol, but good resistance (low solubility) in morpholine and aniline (in disagreement with the Hanson model predictions).