Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Magorrian Relation in Astrophysics

Source Notebook

Relationship between the mass of a black hole and galaxy bulge velocity dispersion

Details

The super massive black hole-velocity dispersion relationship (MBH-σv) is an empirical power law relationship between the mass MMB of the black hole and the velocity dispersion σv of the bulge in the galaxy in which the black hole resides. The super massive black hole is located at the center of the bulge and has a mass that is millions to billions of times the mass of the sun.
On a log scale the Magorrian relationship takes the linear form log10(MBH/108Msun)=a log10(σv/200 km/s)+b where a and b are the slope and intercept of the best fit line. The mass of the sun is denoted by Msun. Sophisticated fits to the Magorrian relationship allow for the possibility of intrinsic dispersion. This means that the scatter around the trend is larger than is expected from measurement errors.
The data here are (x,y) points together with measurement errors in both x and y. They are useful for gaining an understanding the effects of combined xy-error on linear regression fits.

(4 columns, 31 rows)

Examples

Basic Examples (1) 

In[1]:=
xydata = ResourceData[\!\(\* TagBox["\"\<Magorrian Relation in Astrophysics\>\"", #& , BoxID -> "ResourceTag-Magorrian Relation in Astrophysics-Input", AutoDelete->True]\)]
Out[1]=

Organize the data in a matrix format and display the first 9 rows:

In[2]:=
observedX = Normal@xydata[All, 1]; observedErrorX = Normal@xydata[All, 2]; observedY = Normal@xydata[All, 3]; observedErrorY = Normal@xydata[All, 4]; Transpose[{observedX, observedErrorX, observedY, observedErrorY}]; MatrixForm[Take[%, {1, 9}]]
Out[7]=

Visualizations (1) 

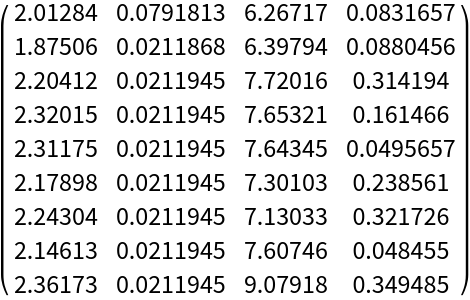A plot of the data with error bars is:

In[8]:=
xydata = ResourceData[\!\(\* TagBox["\"\<Magorrian Relation in Astrophysics\>\"", #& , BoxID -> "ResourceTag-Magorrian Relation in Astrophysics-Input", AutoDelete->True]\)]; observedX = Normal@xydata[All, 1]; observedErrorX = Normal@xydata[All, 2]; observedY = Normal@xydata[All, 3]; observedErrorY = Normal@xydata[All, 4]; pntsLeftX = Transpose[{observedX - observedErrorX, observedY}]; pntsRightX = Transpose[{observedX + observedErrorX, observedY}]; pntsUpY = Transpose[{observedX, observedY + observedErrorY}]; pntsDownY = Transpose[{observedX, observedY - observedErrorY}]; errorLines = Join[Transpose[{pntsLeftX, pntsRightX}], Transpose[{pntsDownY, pntsUpY}] ]; errorLines = {Black, Thin, Map[Line, errorLines]}; ListPlot[Transpose[{observedX, observedY}] , Prolog -> {errorLines} , Sequence[PlotStyle -> { PointSize[0.02]}, PlotRange -> {{1.7, 2.7}, {6, 10}}, FrameLabel -> {"\!\(\*SubscriptBox[\(log\), \(10\)]\)(\!\(\*SubscriptBox[\(\[Sigma]\), \(v\)]\)/200 km/s)", "\!\(\*SubscriptBox[\(log\), \(10\)]\)(\!\(\*SubscriptBox[\(M\), \(BH\)]\)/ \!\(\*SuperscriptBox[\(10\), \(8\)]\)\!\(\*SubscriptBox[\(M\), \(sun\)]\))"}, BaseStyle -> {FontFamily -> "Arial", FontSize -> 14}, Axes -> False, Frame -> True, ImageSize -> 400, AspectRatio -> 1, PlotRange -> All]]
Out[12]=

Analysis (6) 

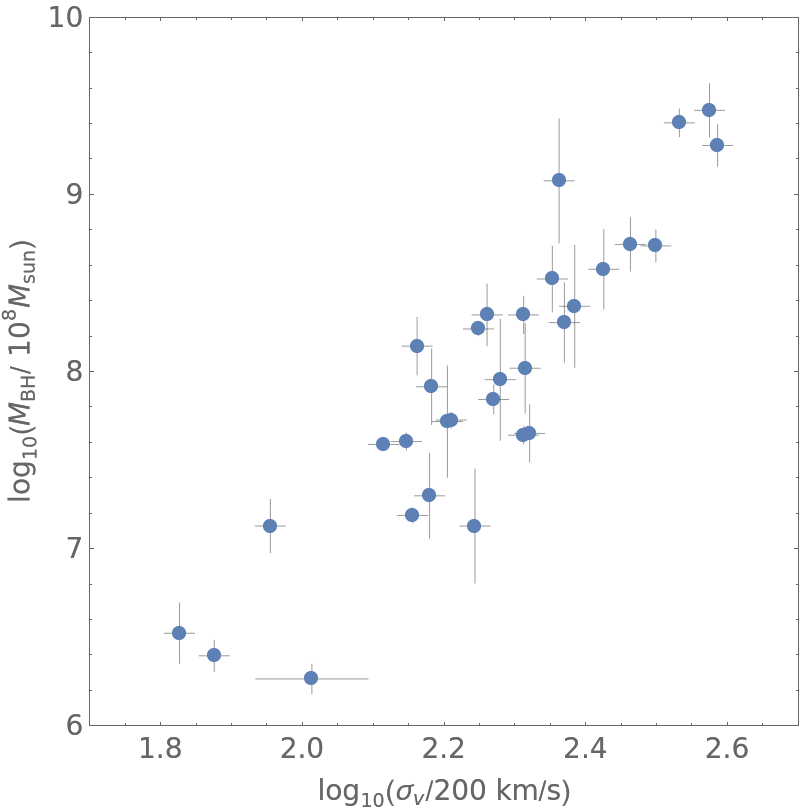We start by acquiring the data that we need:

In[13]:=
xydata = ResourceData[\!\(\* TagBox["\"\<Magorrian Relation in Astrophysics\>\"", #& , BoxID -> "ResourceTag-Magorrian Relation in Astrophysics-Input", AutoDelete->True]\)]; observedX = Normal@xydata[All, 1]; observedErrorX = Normal@xydata[All, 2]; observedY = Normal@xydata[All, 3]; observedErrorY = Normal@xydata[All, 4];

In mathematical terms the likelihood of all n data pairs (xi,yi) and their respective standard deviations (σx,i,σy,i) is as follows:

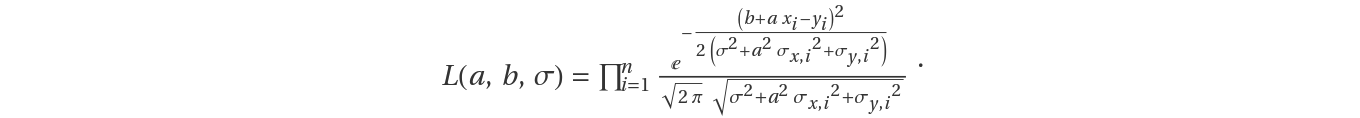
In this expression a is the slope of the best fit line, b is the intercept of the line and σ is the intrinsic dispersion.

The following block of code computes the log likelihood of the data. Computations are performed on a log scale to avoid underflow and overflow:

In[14]:=
Clear[logLikelihood, a, b, \[Sigma]]; logLikelihood[a_, b_, \[Sigma]_] := Module[{x, \[Sigma]x, y, \[Sigma]y, logL}, x = observedX; \[Sigma]x = observedErrorX; y = observedY; \[Sigma]y = observedErrorY; logL = -Length[x] Log[Sqrt[2.0 \[Pi]]] + Sum[-0.5 (y[[i]] - a*x[[i]] - b)^2/(\[Sigma]^2 + a^2 \[Sigma]x[[i]]^2 + \[Sigma]y[[i]]^2) - Log[ Sqrt[\[Sigma]^2 + a^2 \[Sigma]x[[i]]^2 + \[Sigma]y[[i]]^2]], {i, 1, Length[x]}]; logL]

The best fit parameters are in terms of maximum likelihood are:

In[15]:=
Clear[a, b, \[Sigma]]; sol = Quiet@ FindMaximum[{logLikelihood[a, b, \[Sigma]], \[Sigma] > 0}, {a, 3.0}, {b, -1.0}, {\[Sigma], 0.3}]; {aML, bML, \[Sigma]ML} = {a, b, \[Sigma]} /. sol[[2]]
Out[17]=

PLot the best fit line on the data:

In[18]:=
bestFit = {Black, Thick, Line[Table[{x, aML*x + bML}, {x, 1.7, 2.7, 0.1}]]}; pntsLeftX = Transpose[{observedX - observedErrorX, observedY}]; pntsRightX = Transpose[{observedX + observedErrorX, observedY}]; pntsUpY = Transpose[{observedX, observedY + observedErrorY}]; pntsDownY = Transpose[{observedX, observedY - observedErrorY}]; errorLines = Join[Transpose[{pntsLeftX, pntsRightX}], Transpose[{pntsDownY, pntsUpY}] ]; errorLines = {Black, Thin, Map[Line, errorLines]}; ListPlot[Transpose[{observedX, observedY}] , Prolog -> {errorLines, bestFit} , Sequence[PlotStyle -> { PointSize[0.02]}, PlotRange -> {{1.7, 2.7}, {6, 10}}, FrameLabel -> {"\!\(\*SubscriptBox[\(log\), \(10\)]\)(\!\(\*SubscriptBox[\(\[Sigma]\), \(v\)]\)/200 km/s)", "\!\(\*SubscriptBox[\(log\), \(10\)]\)(\!\(\*SubscriptBox[\(M\), \(BH\)]\)/ \!\(\*SuperscriptBox[\(10\), \(8\)]\)\!\(\*SubscriptBox[\(M\), \(sun\)]\))"}, BaseStyle -> {FontFamily -> "Arial", FontSize -> 14}, Axes -> False, Frame -> True, ImageSize -> 400, AspectRatio -> 1, PlotRange -> All]]
Out[25]=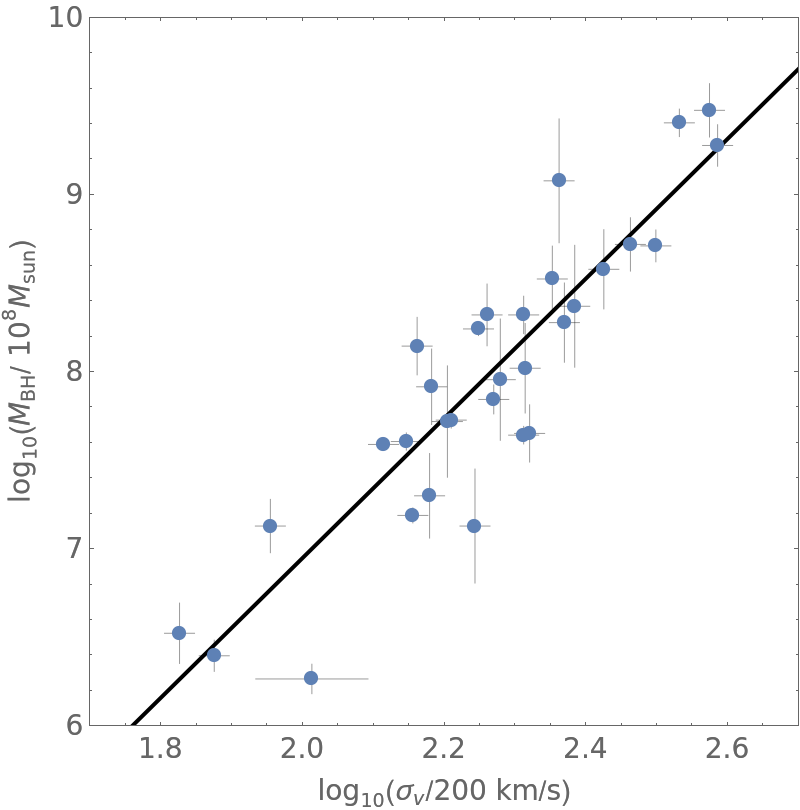

Marshall Bradley, "Magorrian Relation in Astrophysics" from the Wolfram Data Repository (2022)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • Andreon, Stefano and Weaver, Brian (2015), Bayesian Methods for the Physical Sciences : Learning from Examples in Astronomy, Springer.

Publisher Information

  • Prepared for the Wolfram Data Repository By: Marshall Bradley
  • Publisher of Record: Marshall Bradley