Analysis (10)
The focus here is on comparing the Poisson fit to the negative binomial fit. Goodness of fit is measured via a comparison of the Bayesian evidence favoring each of the two models.
Read in the data and find the mean:
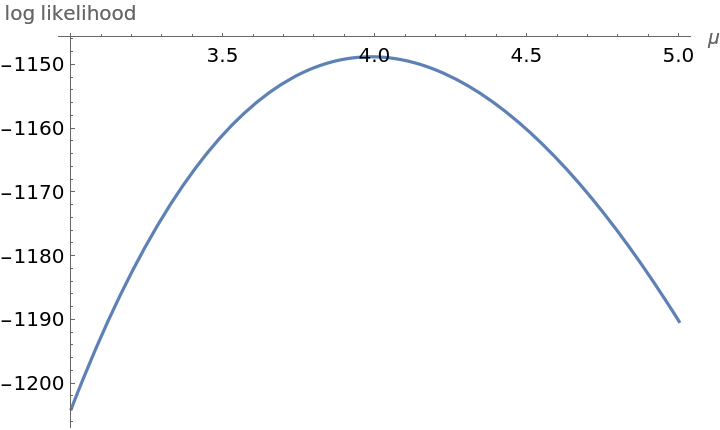
The Poisson random variable has one parameter namely the mean μ. Plot the log likelihood of the data under the assumption that it is Poisson distributed:
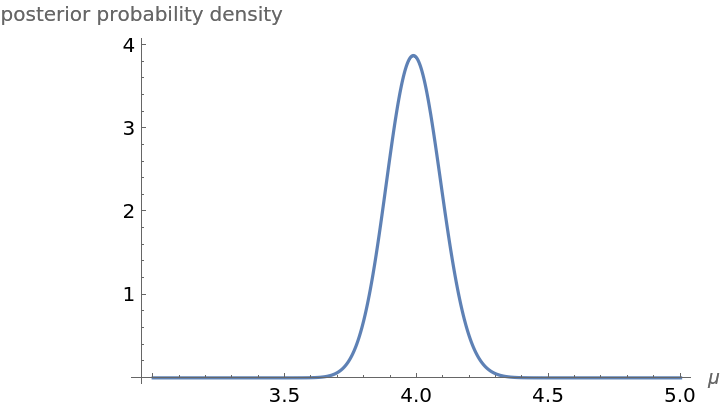
Plot the posterior probability density function for the parameter μ under the assumption that the prior probability distribution for μ is flat on the interval (μmin,μmax). Bayes theorem tell us that the posterior probability distribution is proportional to the product of the prior and the likelihood. The constant of proportionality known as the evidence and is found by numerical integration. Computations are performed on a log scale to avoid numerical underflow:
Compute the Bayesian evidence in favor of the Poisson model:
The Bayesian evidence is only meaningful when compared to another model using the exact same data.
Now we turn our attention to the evidence computation of the negative binomial assumption. The negative binomial distribution has two unknown parameters r and p. The log likelihood of the data under the assumption of the negative binomial distribution is:
The evidence computation requires an integration over two dimensions. We assume that on prior information r is flat distributed on (0.1,5.0) and that p is flat distributed on (0.05,0.5). The results of the evidence computation are:
As a check compute the evidence using the function NItegrate:
The difference between the evidence in favor of the negative binomial model and the Poisson model is huge. The observed data clearly favor the negative binomial model relative to the Poisson model:
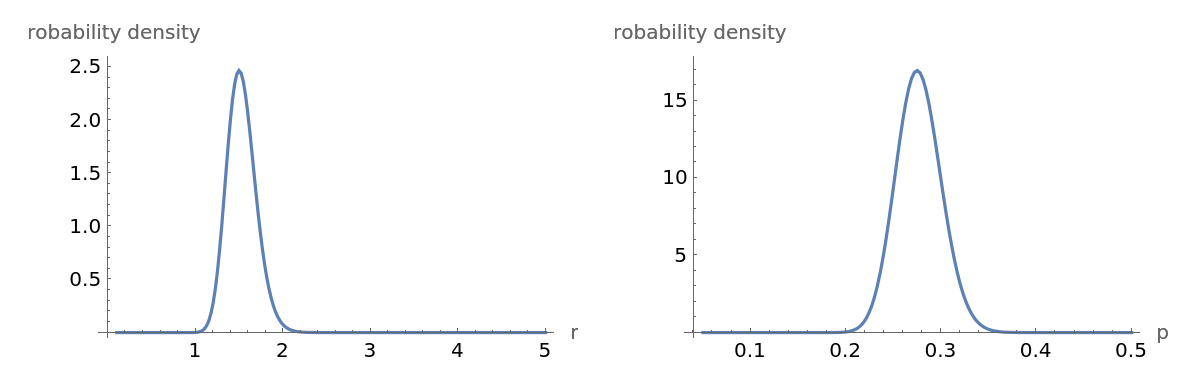
All the information in a Bayesian analysis is in the posterior. The posterior marginal probability density function for the parameters r and p are:
These two marginal probability density functions are clearly consistent with results from the function EstimatedDistribution:

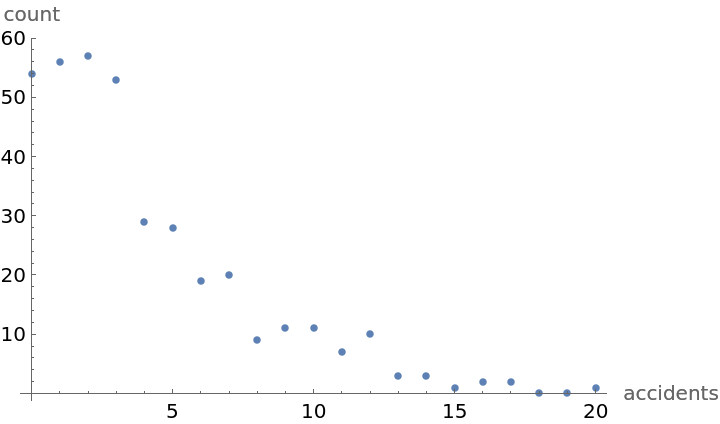
![dataset = ResourceData[\!\(\*
TagBox["\"\<Negative Binomial Distributed Accident Data\>\"",
#& ,
BoxID -> "ResourceTag-Negative Binomial Distributed Accident Data-Input",
AutoDelete->True]\)];
number = Table[dataset[[i]][[1]], {i, 1, 21}];
observed = Table[dataset[[i]][[2]], {i, 1, 21}];
ListPlot[Transpose[{number, observed}], AxesLabel -> {"accidents", "count"}]](https://www.wolframcloud.com/obj/resourcesystem/images/f0c/f0c80de3-d773-4917-ae05-5599ef7de4d2/672601dfd0d9d775.png)
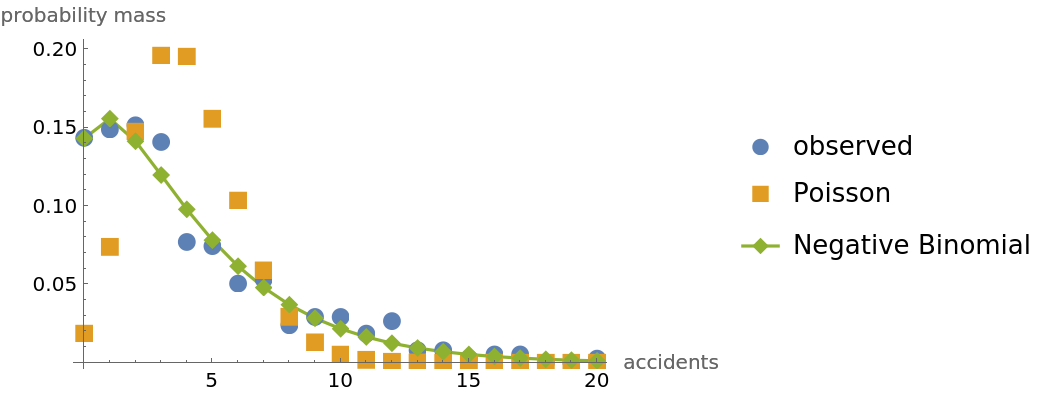
![dataset = Dataset[ResourceData[\!\(\*
TagBox["\"\<Negative Binomial Distributed Accident Data\>\"",
#& ,
BoxID -> "ResourceTag-Negative Binomial Distributed Accident Data-Input",
AutoDelete->True]\)]];
observed = Table[dataset[[i]][[2]], {i, 1, 21}];
observations = Flatten@Table[Table[i - 1, {observed[[i]]}], {i, 1, 21}];
Clear[\[Mu], r, p];
distPoisson = EstimatedDistribution[observations, PoissonDistribution[\[Mu]]];
distNB = EstimatedDistribution[observations, NegativeBinomialDistribution[r, p]];
empiricalPDF = N@Transpose[{number, observed/Total[observed]}];
theoPoisson = Table[{r, PDF[distPoisson, r]}, {r, 0, 20, 1}];
theoNB = Table[{r, PDF[distNB, r]}, {r, 0, 20, 1}];
ListPlot[{empiricalPDF, theoPoisson, theoNB}, Sequence[
PlotLegends -> {"observed", "Poisson", "Negative Binomial"}, PlotMarkers -> {Automatic, Medium}, Joined -> {False, False, True}, AxesLabel -> {"accidents", "probability mass"}]]](https://www.wolframcloud.com/obj/resourcesystem/images/f0c/f0c80de3-d773-4917-ae05-5599ef7de4d2/13878052376d2fd1.png)
![dataset = Dataset[ResourceData[\!\(\*
TagBox["\"\<Negative Binomial Distributed Accident Data\>\"",
#& ,
BoxID -> "ResourceTag-Negative Binomial Distributed Accident Data-Input",
AutoDelete->True]\)]];
observed = Table[dataset[[i]][[2]], {i, 1, 21}];
observations = Flatten@Table[Table[i - 1, {observed[[i]]}], {i, 1, 21}];
\[Mu]observed = N@Mean[observations]](https://www.wolframcloud.com/obj/resourcesystem/images/f0c/f0c80de3-d773-4917-ae05-5599ef7de4d2/3e1a3af49c1fe2ec.png)
![Clear[\[Mu]];
logLikelihoodPoisson[\[Mu]_] := N@Sum[observed[[
m + 1]] (m*Log[\[Mu]] - \[Mu] - Log[Factorial[m]]), {m, 0, 20}]
Plot[logLikelihoodPoisson[\[Mu]], {\[Mu], 3.0, 5.0}, AxesLabel -> {"\[Mu]", "log likelihood"}]](https://www.wolframcloud.com/obj/resourcesystem/images/f0c/f0c80de3-d773-4917-ae05-5599ef7de4d2/0017a20d7ab6edd6.png)
![\[Mu]min = 3.0; \[Mu]max = 5.0; d\[Mu] = 0.0025;
logpdf = Table[Log[1/(\[Mu]max - \[Mu]min)] + logLikelihoodPoisson[\[Mu]], {\[Mu], \[Mu]min, \[Mu]max, d\[Mu]}];
maxlog = Max[logpdf];
logpdf = logpdf - maxlog; pdf = Exp[logpdf];
pdf = (d\[Mu]^-1) pdf/Total[pdf];
ListLinePlot[pdf, Sequence[
PlotRange -> All, DataRange -> {\[Mu]min, \[Mu]max}, AxesLabel -> {"\[Mu]", "posterior probability density"}]]](https://www.wolframcloud.com/obj/resourcesystem/images/f0c/f0c80de3-d773-4917-ae05-5599ef7de4d2/58424ec3e82fd3d1.png)
![\[Mu]min = 3.0; \[Mu]max = 5.0; d\[Mu] = 0.0025;
logpdf = Table[Log[1/(\[Mu]max - \[Mu]min)] + logLikelihoodPoisson[\[Mu]], {\[Mu], \[Mu]min, \[Mu]max, d\[Mu]}];
maxlog = Max[logpdf];
logpdf = logpdf - maxlog; posterior = Exp[logpdf];
logEvidencePoisson = Log[d\[Mu]*Total[posterior]] + maxlog](https://www.wolframcloud.com/obj/resourcesystem/images/f0c/f0c80de3-d773-4917-ae05-5599ef7de4d2/229cc02d260a48b5.png)
![rmin = 0.1; rmax = 5.0; nr = 201;
pmin = 0.05; pmax = 0.5; np = 151;
dr = (rmax - rmin)/(nr - 1); dp = (pmax - pmin)/(np - 1);
loggrid2d = Table[Log[1/(rmax - rmin) 1/(pmax - pmin)] + logLikelihoodNB[r, p], {r, rmin, rmax, dr}, {p, pmin, pmax, dp}];
maxlog = Max[Flatten[loggrid2d]];
loggrid2d = ArrayReshape[Flatten[loggrid2d] - maxlog, Dimensions[loggrid2d]];
logEvidenceNB = maxlog + Log[dp*dr*Total[Exp[Flatten[loggrid2d]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/f0c/f0c80de3-d773-4917-ae05-5599ef7de4d2/5cfb71f23244398d.png)
![loggrid = Table[logLikelihoodNB[r, p], {r, rmin, rmax, dr}, {p, pmin, pmax, dp}];
lmax = Max[loggrid];
Quiet[NIntegrate[
1/(rmax - rmin) 1/(pmax - pmin) Exp[
logLikelihoodNB[r, p] - lmax], {r, rmin, rmax}, {p, pmin, pmax}]];
Log[%] + lmax](https://www.wolframcloud.com/obj/resourcesystem/images/f0c/f0c80de3-d773-4917-ae05-5599ef7de4d2/61bf9c927f7d4e29.png)
![posteriorPDF = Exp[loggrid2d];
posteriorPDF = 1/(dp*dr) (posteriorPDF/Total[Flatten[posteriorPDF]]);
pdfr = dp*Chop@Map[Total, Map[Flatten, posteriorPDF]];
pdfp = dr*Chop@Map[Total, Map[Flatten, Transpose[posteriorPDF]]];
gr = ListLinePlot[pdfr, DataRange -> {rmin, rmax}, PlotRange -> All, AxesLabel -> {"r", "probability density"}];
gp = ListLinePlot[pdfp, DataRange -> {pmin, pmax}, PlotRange -> All, AxesLabel -> {"p", "probability density"}];
GraphicsRow[{gr, gp}]](https://www.wolframcloud.com/obj/resourcesystem/images/f0c/f0c80de3-d773-4917-ae05-5599ef7de4d2/163d8345f70a6f43.png)