Wolfram Research

Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Periodic Patterns

Source Notebook

A list of binary and ternary periodic pattern generators grouped by colors and periodicity

Details

Patterns are given as generators for ResourceFunction["PeriodicPatternGenerator"][n,{x,y},disp:0,b:2]: Create a periodic square array with side length of x×y based on an x×y rectangle filled with the digits of integer n in base 2 (or b), where the rectangle is repeated on subsequent rows with displacement disp.
Periodic patterns can be equivalent by toroidal displacement. For example, an 8×8 checkerboard pattern with a black square in the lower right corner is equivalent to an 8×8 checkerboard pattern with a white square in the lower right corner after a toroidal displacement of {a,b} for any odd a+b.
Periodic patterns similar by rotations, reflections, color reversals and skew displacement are considered distinct in these datasets.
For the counts below, an n-ary pattern is assumed to have n colors. An exception is made for binary, where order 1 has both all 0 and all 1 tilings.
Up to order 16, there are 2, 3, 8, 20, 36, 112, 144, 452, 740, 1824, 2232, 9848, 8820, 28302, 54015, 129064 distinct binary patterns.
Up to order 10, there are 0, 0, 8, 65, 180, 1123, 2064, 11391, 27187, 104774 distinct ternary patterns.

Examples

Basic Examples (2) 

Retrieve the order 3 binary periodic pattern generators:

In[1]:=
order3 = ResourceData[\!\(\* TagBox["\"\<Periodic Patterns\>\"", #& , BoxID -> "ResourceTag-Periodic Patterns-Input", AutoDelete->True]\)][{3, 2}]
Out[1]=

Show all eight order 3 binary periodic patterns:

In[2]:=
Grid[Partition[Column[{#, ArrayPlot[ArrayFlatten[Table[ ResourceFunction["PeriodicPatternGenerator"][#], {3}, {3}]], PixelConstrained -> 10, Mesh -> {8, 8}]}] & /@ order3, 4], Frame -> All]
Out[2]=

Retrieve generators for order 5 binary periodic patterns:

In[3]:=
order5 = ResourceData[\!\(\* TagBox["\"\<Periodic Patterns\>\"", #& , BoxID -> "ResourceTag-Periodic Patterns-Input", AutoDelete->True]\)][{5, 2}]
Out[3]=

Show the binary order 5 periodic patterns with generators as tooltips:

In[4]:=
Grid[Partition[ Tooltip[ArrayPlot[ ArrayFlatten[ Table[ResourceFunction[ "PeriodicPatternGenerator"][#], {2}, {2}]], PixelConstrained -> 6, Mesh -> {9, 9}], #] & /@ order5, 6], Frame -> All]
Out[4]=

Scope & Additional Elements (3) 

Show the order 5 binary patterns as matrices:

In[5]:=
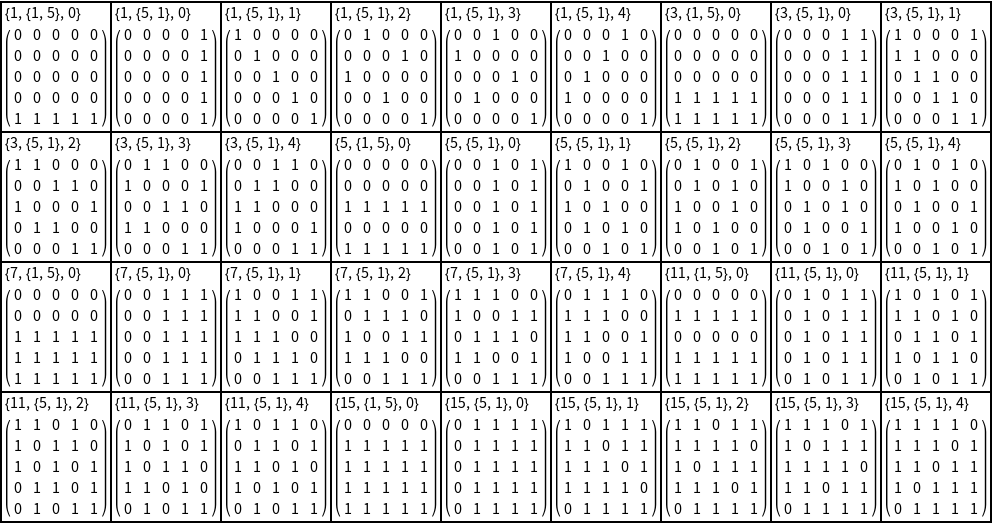
Style[Grid[ Partition[ Column[{#, MatrixForm[ ResourceFunction["PeriodicPatternGenerator"][#], #]}] & /@ ResourceData[\!\(\* TagBox["\"\<Periodic Patterns\>\"", #& , BoxID -> "ResourceTag-Periodic Patterns-Input", AutoDelete->True]\)][{5, 2}], 9], Frame -> All], 8]
Out[5]=

Show samples of the 129064 order 16 binary patterns:

In[6]:=
Grid[Partition[Tooltip[ArrayPlot[ArrayFlatten[Table[ ResourceFunction["PeriodicPatternGenerator"][#], {2}, {2}]], PixelConstrained -> 3, Frame -> False], #] & /@ RandomSample[ResourceData[\!\(\* TagBox["\"\<Periodic Patterns\>\"", #& , BoxID -> "ResourceTag-Periodic Patterns-Input", AutoDelete->True]\)][{16, 2}], 25], 5], Frame -> All]
Out[6]=

The 65 order-4 ternary periodic patterns:

In[7]:=
Grid[Partition[ Tooltip[ArrayPlot[ ArrayFlatten[ Table[ResourceFunction[ "PeriodicPatternGenerator"][#], {2}, {2}]], PixelConstrained -> 5, Mesh -> {7, 7}], #] & /@ ResourceData[\!\(\* TagBox["\"\<Periodic Patterns\>\"", #& , BoxID -> "ResourceTag-Periodic Patterns-Input", AutoDelete->True]\)][{4, 3}], 13]]
Out[7]=

Wolfram Research, "Periodic Patterns" from the Wolfram Data Repository (2022)  

Data Resource History

  • Date Created:

Source Metadata

  • Creator: Ed Pegg Jr
  • Citation: Source, reference or citation information

See Also

Publisher Information

  • Prepared for the Wolfram Data Repository By: Ed Pegg Jr
  • Publisher of Record: Wolfram Research