Primitive polynomials for Galois field generation up to GF(2^1200), GF(3^660), GF(5^430), and GF(7^358)
Examples
Basic Examples
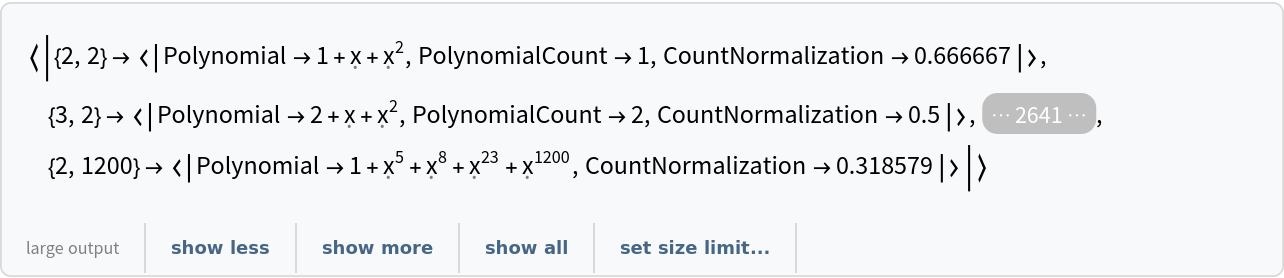
Retrieve the default content:
Visual Examples
Show the data for GF(267). The number 267-1 has a factorization 193707721×761838257287 (Cole, 1903) that gives a normalization close to 1:
Generate the first 600 powers of x using a polynomial modulus of 1+x+x2+x5+x67:
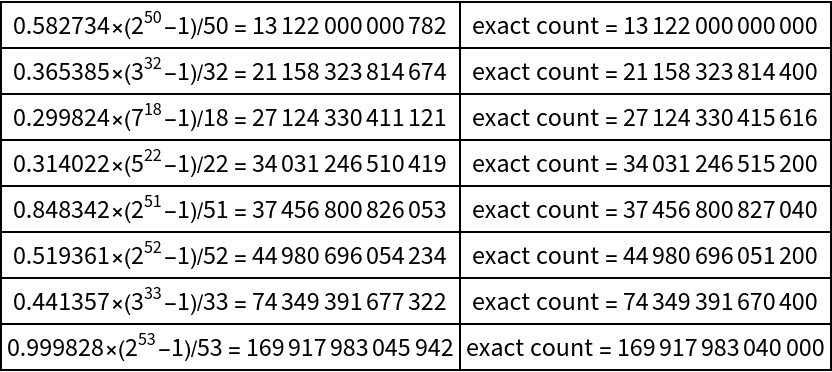
Show the approximate count via multiplication of the count normalization by (pn-1)/n and compare that to the actual polynomial count:
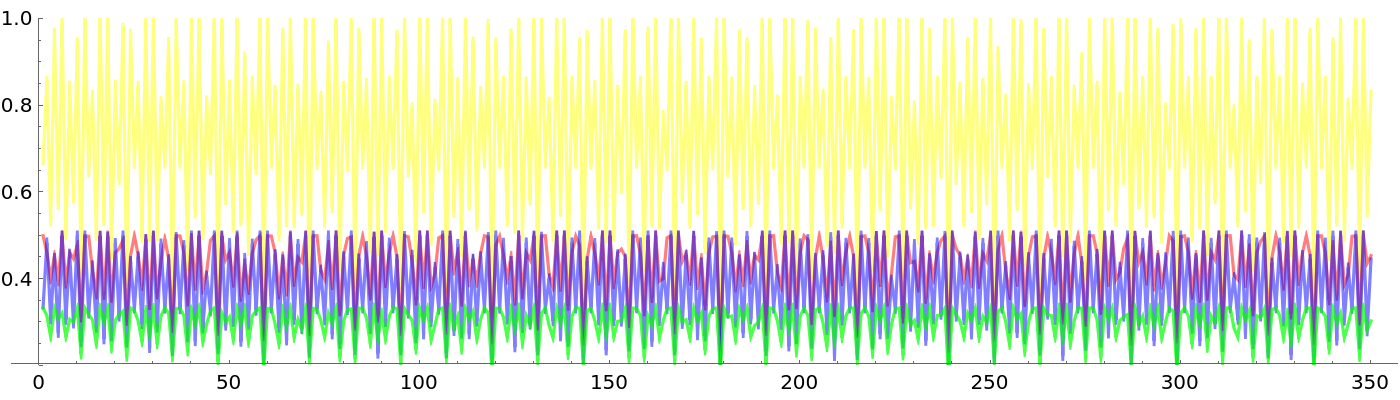
Show the count normalizations for the first four primes:
Show the degrees where trinomial primitive polynomials exist for the first four primes:
Bibliographic Citation
Wolfram Research,
"Primitive Polynomials"
from the Wolfram Data Repository
(2017)
https://doi.org/10.24097/wolfram.48521.data
Data Resource History
Data Downloads
Publisher Information
![With[{data = ResourceData["Primitive Polynomials"]}, ArrayPlot[
Transpose[
Table[PadRight[
CoefficientList[
PolynomialMod[\[FormalX]^n, {data[{2, 67}]["Polynomial"], 2}], \[FormalX]], 67, 0], {n, 1, 600}]], Frame -> False, ImageSize -> {610, 70}, PixelConstrained -> True]]](https://www.wolframcloud.com/obj/resourcesystem/images/028/0282c399-a696-427e-91e1-2d31f8a686e1/3a107523e0b6d123.png)

![Grid[{Row[{ NumberForm[#[[2]]["CountNormalization"], {7, 6}, NumberPadding -> {"", "0"}], "\[Times](", Superscript[#[[1, 1]], #[[1, 2]]], "-1)/", #[[1, 2]], " = ", Round[#[[2]][
"CountNormalization"] (#[[1, 1]]^#[[1, 2]] - 1)/#[[1, 2]]] }], Row[{ "exact count = ", #[[2]]["PolynomialCount"]}]} & /@ SortBy[Select[Normal[ResourceData["Primitive Polynomials"]], 10^15 < #[[1, 1]]^#[[1, 2]] < 10^16 &], #[[2]][
"PolynomialCount"] &], Frame -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/028/0282c399-a696-427e-91e1-2d31f8a686e1/64a523ec2b04dd60.png)
![ListPlot[
Table[#[[2]]["CountNormalization"] & /@ Take[Select[
Normal[ResourceData["Primitive Polynomials"]], #[[1, 1]] == Prime[n] &], 350], {n, 1, 4}], AspectRatio -> 1/4, ImageSize -> {700, 200}, PlotRange -> {.2, 1}, Joined -> True, PlotStyle -> {{Opacity[.5], Yellow}, {Opacity[.5], Red}, {Opacity[.5], Blue}, {Opacity[.7], Green}}]](https://www.wolframcloud.com/obj/resourcesystem/images/028/0282c399-a696-427e-91e1-2d31f8a686e1/419ac4f29acba8a0.png)
![Text@Grid[
Prepend[Prepend[Table[data[{Prime[n], #}]["Polynomial"], {n, 1, 4}],
Style[#, 16]] & /@
Select[Range[2, 60], Max[Table[
Length[data[{Prime[n], #}]["Polynomial"]], {n, 1, 4}]] == 3 &], Prepend[Table[Style[Prime[n], 20], {n, 1, 4}], Spacer[5]]]]](https://www.wolframcloud.com/obj/resourcesystem/images/028/0282c399-a696-427e-91e1-2d31f8a686e1/1b2d300b68bc57ba.png)
