Wolfram Data Repository
Immediate Computable Access to Curated Contributed Data
Radioactive Isotope Half Lives
Half lives in seconds for 1175 radioactive isotopes
Details
The data set contains the half lives for 1175 radioactive isotopes. The data set is organized alphabetically by isotope name. The format of each entry is {isotope name,x,y}. The corresponding half life in seconds for the entry is t1/2=x 10y. The first entry in the data set is actinium-205 with x=20 and y=-3. So the half life for this entry is 20⨯10-3 sec. The time span in the data det is enormous with the the exponent y varying from -24 to 31 in steps of 3. The statistical disribution of first digits of the isotope half lives, eg. 2 for actinium-205, closely follows Benford's law. The first digit 1 is much more common than 9. This will hold true even if the time unit is changed from seconds to hours, days or years.
Examples
Basic Examples (1)
Retrieve the data and present the the data in a tabular format:
| In[1]:= | ![ResourceData[\!\(\*
TagBox["\"\<Radioactive Isotope Half Lives\>\"",
#& ,
BoxID -> "ResourceTag-Radioactive Isotope Half Lives-Input",
AutoDelete->True]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/eec/eec66a63-6de1-4dfe-839a-afeed6e3a377/0960f179080fd24d.png){kind=small} |
| Out[1]= |  |
Visualizations (1)
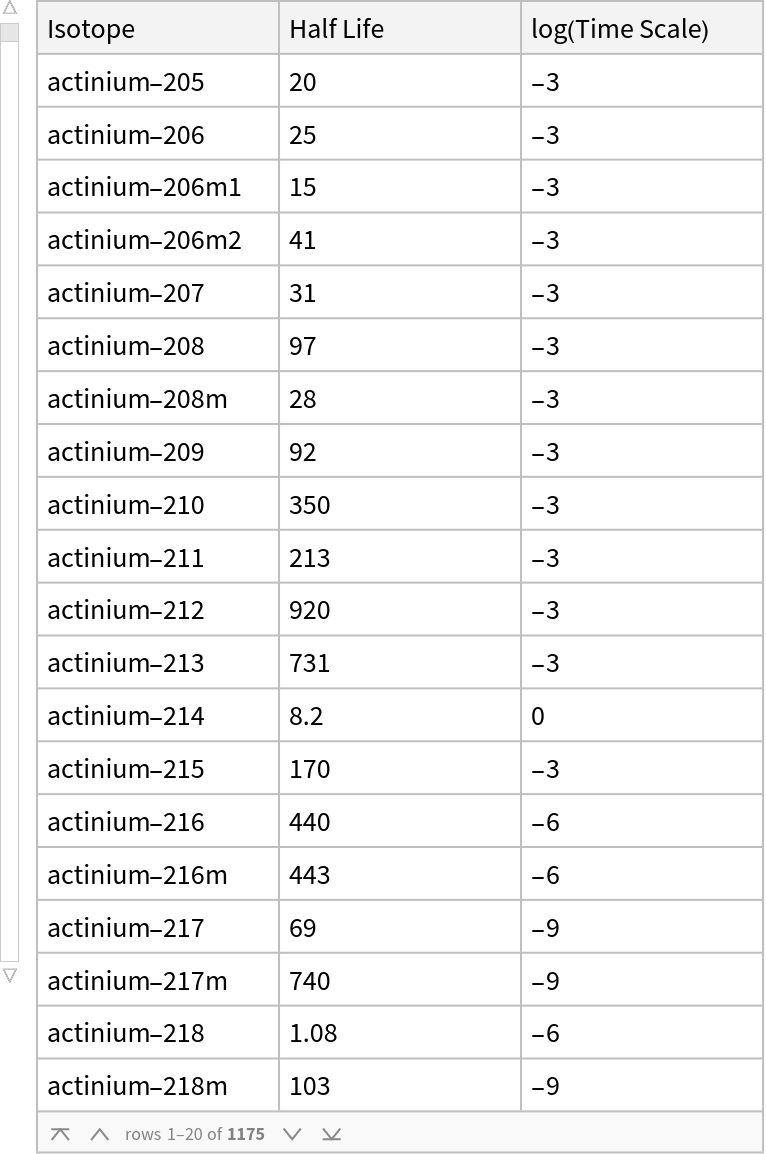Display all entries in the data set for the element bismuth with half lives in seconds converted to a log scale:
| In[2]:= | ![element = "bismuth";
dataset = ResourceData[\!\(\*
TagBox["\"\<Radioactive Isotope Half Lives\>\"",
#& ,
BoxID -> "ResourceTag-Radioactive Isotope Half Lives-Input",
AutoDelete->True]\)];
name = dataset[All, "Isotope"] // Normal;
x = dataset[All, "Half Life"] // Normal; y = dataset[All, "log(Time Scale)"] // Normal;
{elmnt, iso} = Transpose[Map[StringSplit[#, "-"] &, name]];
data = Transpose[{elmnt, iso, Log[10, N[x*10^y]]}]; data = Select[data, #[[1]] == element &];
temp = Table[<|"Element" -> data[[i]][[1]], "Isotope Number" -> data[[i]][[2]], "Log[10,Half Life (sec)]" -> data[[i]][[3]]|>, {i, 1, Length[data]}];
Dataset[temp, ItemSize -> 18]](https://www.wolframcloud.com/obj/resourcesystem/images/eec/eec66a63-6de1-4dfe-839a-afeed6e3a377/519302d69a2ab724.png) |
| Out[9]= |  |
Analysis (1)
The following block of code compares the observed distribution of first digits in the half life data set to the theoretical Bedford distribution. The agreement is quite good:
| In[10]:= | ![dataset = ResourceData[\!\(\*
TagBox["\"\<Radioactive Isotope Half Lives\>\"",
#& ,
BoxID -> "ResourceTag-Radioactive Isotope Half Lives-Input",
AutoDelete->True]\)];
firstdigits = dataset[All, "Half Life"] // Normal;
firstdigit = Map[ToExpression, Map[First, Map[Characters, Map[ToString, firstdigits]]]];
counts = Table[Count[firstdigit, i], {i, 1, 9}];
measured = N@counts/Total[counts];
theoretical = Map[Point, N@Table[{i, Log[10, (i + 1)/i]}, {i, 1, 9}]];
ref = Line[Table[{i, Log[10, (i + 1)/i]}, {i, 1, 9, 0.01}]];
BarChart[measured, Epilog -> {PointSize[0.025], theoretical, ref}, PlotRange -> {0, 0.350}, ChartLabels -> Placed[{1, 2, 3, 4, 5, 6, 7, 8, 9}, Bottom]]](https://www.wolframcloud.com/obj/resourcesystem/images/eec/eec66a63-6de1-4dfe-839a-afeed6e3a377/674634d08954b2d0.png) |
| Out[17]= |  |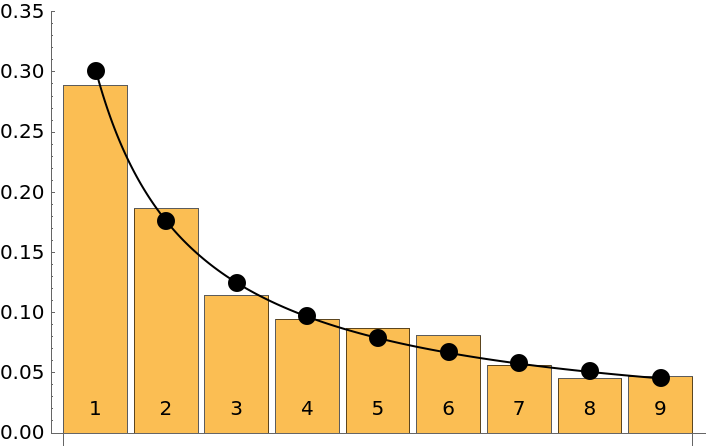
Bibliographic Citation
Marshall Bradley, "Radioactive Isotope Half Lives" from the Wolfram Data Repository (2024)