Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Regular Computational Complexity Graph

Source Notebook

WWW Graph of Computational Complexity for Link Analysis Ranking Experiments

WWW Graph of Computational Complexity for Link Analysis Ranking Experiments: The Base Set is constructed by including only the first 50 out-links of each Root page. We use the simple algorithm for detecting intra-domain links.

(832 vertices, 1555 edges)

Examples

Basic Examples

Retrieve the graph:

In[1]:=
ResourceData["Regular Computational Complexity Graph"]
Out[1]=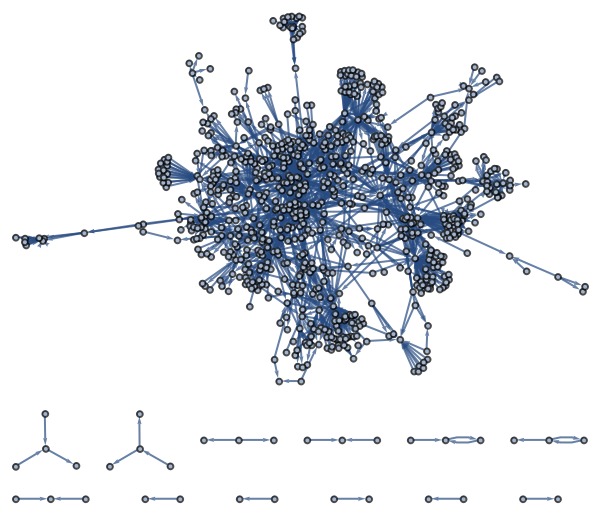

Summary properties:

In[2]:=
ResourceData["Regular Computational Complexity Graph", All]["Summary"]
Out[2]=

Basic Applications

Show the power-law degree distribution of the graph:

In[3]:=
g = ResourceData["Regular Computational Complexity Graph"];
In[4]:=
Histogram[VertexDegree[g], {"Log", {1, 1000, 5}}, {"Log", "PDF"}, AxesLabel -> { "Degree \!\(\*\nStyleBox[\"k\",\nFontSlant->\"Italic\"]\)", "\!\(\*SubscriptBox[\(p\), \(k\)]\)"}]
Out[4]=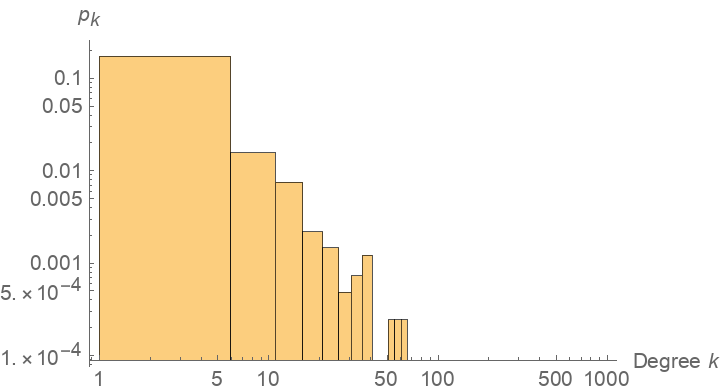

Show a table of properties:

In[5]:=
Dataset[Table[<| i -> i[g]|>, {i, {GraphReciprocity, GlobalClusteringCoefficient, GraphAssortativity}}]]
Out[5]=

Wolfram Research, "Regular Computational Complexity Graph" from the Wolfram Data Repository (2019)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • Datasets for Experiments on Link Analysis Ranking Algorithms, "http://www.cs.toronto.edu/~tsap/experiments/datasets/index.html"

Data Downloads

Publisher Information

  • Prepared for the Wolfram Data Repository By: Wolfram
  • Publisher of Record: Wolfram Research