Wolfram Data Repository
Immediate Computable Access to Curated Contributed Data
Repetition Periods for Elementary Cellular Automata
A collection of rules and their repetition periods as a function of size
Originator: Stephen Wolfram
A plot of these repetition periods as originally provided on page 260 of A New Kind of Science (Wolfram, 2002) and a visualization was provided on page 259
(2 columns, 5 rows)
Examples
Basic Examples (1)
View the data:
| In[1]:= | ![ResourceData[\!\(\*
TagBox["\"\<Repetition Periods for Elementary Cellular Automata\>\"",
#& ,
BoxID -> "ResourceTag-Repetition Periods for Elementary Cellular Automata-Input",
AutoDelete->True]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/937/9374364c-0703-4eb8-92c6-91c045253d70/188a2fac4ba4ec38.png){kind=small} |
| Out[1]= |  |
Visualization (4)
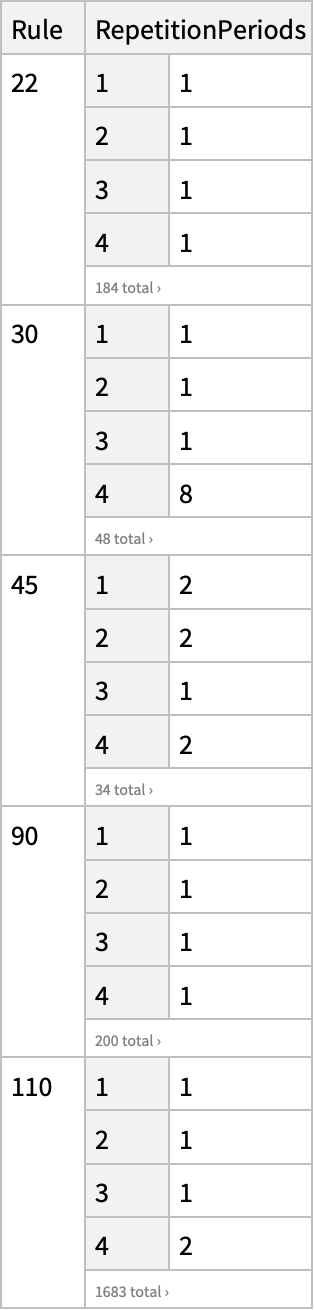Find the systems provided:
| In[2]:= | ![Normal@ResourceData[\!\(\*
TagBox["\"\<Repetition Periods for Elementary Cellular Automata\>\"",
#& ,
BoxID -> "ResourceTag-Repetition Periods for Elementary Cellular Automata-Input",
AutoDelete->True]\)][[All, "Rule"]]](https://www.wolframcloud.com/obj/resourcesystem/images/937/9374364c-0703-4eb8-92c6-91c045253d70/0e3e089f6610a38c.png){kind=small} |
| Out[2]= |  |
Find the systems sizes for rule 90 with repetition period between 5 and 50:
| In[3]:= | ![Select[Select[Normal@ResourceData[\!\(\*
TagBox["\"\<Repetition Periods for Elementary Cellular Automata\>\"",
#& ,
BoxID -> "ResourceTag-Repetition Periods for Elementary Cellular Automata-Input",
AutoDelete->True]\)], #Rule == 90 &][[1, "RepetitionPeriods"]], Between@{5, 50}]](https://www.wolframcloud.com/obj/resourcesystem/images/937/9374364c-0703-4eb8-92c6-91c045253d70/741240f5443836e9.png) |
| Out[3]= |  |
Plot these:
| In[4]:= | ![Module[{rule = 90, repetitionPeriods}, repetitionPeriods = Select[Normal@ResourceData[\!\(\*
TagBox["\"\<Repetition Periods for Elementary Cellular Automata\>\"",
#& ,
BoxID -> "ResourceTag-Repetition Periods for Elementary Cellular Automata-Input",
AutoDelete->True]\)], #Rule == rule &][[1, "RepetitionPeriods"]]; Table[ArrayPlot@
CellularAutomaton[rule, ReplacePart[ConstantArray[0, n], Ceiling@(n/2) -> 1], 100], {n, Keys@Reverse@Sort@Select[repetitionPeriods, Between@{5, 50}] // Take[#, UpTo[5]] &}]]](https://www.wolframcloud.com/obj/resourcesystem/images/937/9374364c-0703-4eb8-92c6-91c045253d70/43f8d4fd00cbc2d4.png) |
| Out[4]= |  |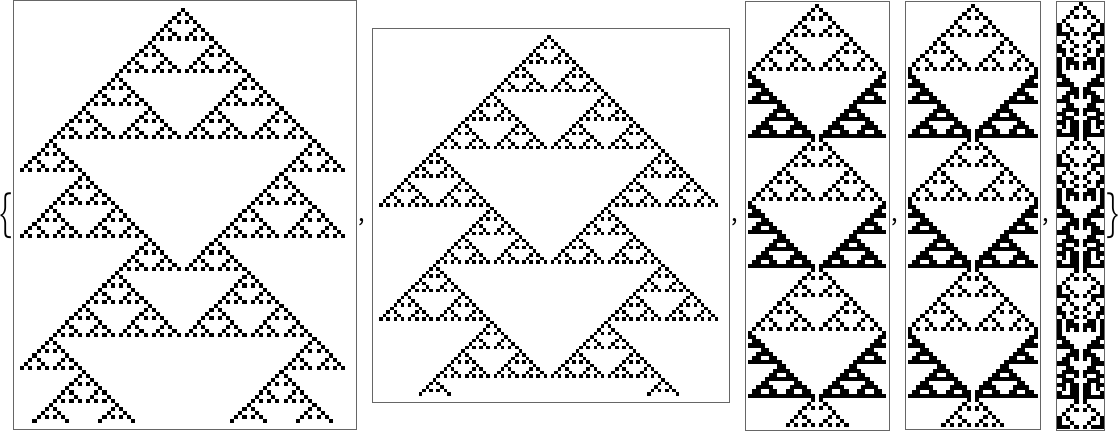
Highlight the repeating blocks:
| In[5]:= | ![Module[{rule = 90, repetitionPeriods, repBlock, firstRep, evolution}, repetitionPeriods = Select[Normal@ResourceData[\!\(\*
TagBox["\"\<Repetition Periods for Elementary Cellular Automata\>\"",
#& ,
BoxID -> "ResourceTag-Repetition Periods for Elementary Cellular Automata-Input",
AutoDelete->True]\)], #Rule == rule &][[1, "RepetitionPeriods"]]; Table[evolution = CellularAutomaton[rule, ReplacePart[ConstantArray[0, n], Ceiling@(n/2) -> 1], 100]; firstRep = FirstCase[
Range[100], _?(# <= (100 - repetitionPeriods[n]) && evolution[[#]] == evolution[[repetitionPeriods[n] + #]] &)]; ArrayPlot[
ReplacePart[evolution, firstRep | _?(# >= firstRep && Mod[# - firstRep + 1, repetitionPeriods[n]] == 0 &) -> Table[2, n]], ColorRules -> {1 -> GrayLevel[0.1], 2 -> Hue[.6, 1, 1]}], {n, Keys@Reverse@Sort@Select[repetitionPeriods, Between@{5, 50}] // Take[#, UpTo@5] &}]]](https://www.wolframcloud.com/obj/resourcesystem/images/937/9374364c-0703-4eb8-92c6-91c045253d70/4cb34ec337b3bdaf.png) |
| Out[5]= |  |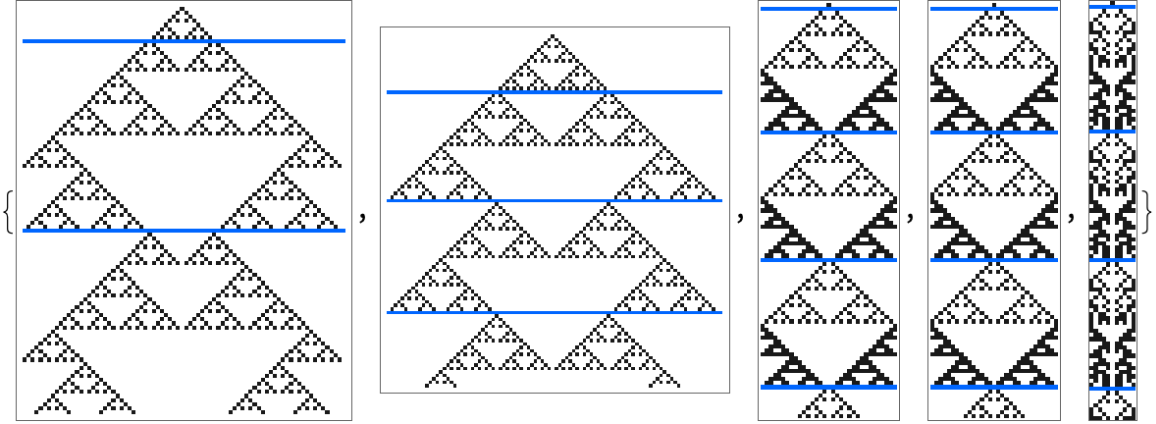
External Links
Bibliographic Citation
Wolfram Research, "Repetition Periods for Elementary Cellular Automata" from the Wolfram Data Repository (2017) https://doi.org/10.24097/wolfram.75508.data