Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Sample Data: London Cholera

Source Notebook

Locations of the 1854 London cholera outbreak near Golden Square

Details

Locations of the 1854 London cholera outbreak near Golden Square in the observation region GeoBoundsRegion[{{51.51065909836119`, 51.51581097178905`}, {-0.14008439736259973`, -0.13222907147321172`}}], annotated with marks including the number of cases, distance (in meters) to the contaminated Broad Street water pump, distance (in meters) to a non-Broad Street pump, and whether or not the Broad Street pump was the closest pump.

Examples

Basic Examples (1) 

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Sample Data: London Cholera\>\"", #& , BoxID -> "ResourceTag-Sample Data: London Cholera-Input", AutoDelete->True]\), "Data"]
Out[1]=

Summary of the spatial point data:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<Sample Data: London Cholera\>\"", #& , BoxID -> "ResourceTag-Sample Data: London Cholera-Input", AutoDelete->True]\), "Data"]["Summary"]
Out[2]=

Visualizations (2) 

Plot the locations:

In[3]:=
GeoListPlot[ResourceData[\!\(\* TagBox["\"\<Sample Data: London Cholera\>\"", #& , BoxID -> "ResourceTag-Sample Data: London Cholera-Input", AutoDelete->True]\), "Data"], GeoBackground -> "VectorMonochrome"]
Out[3]=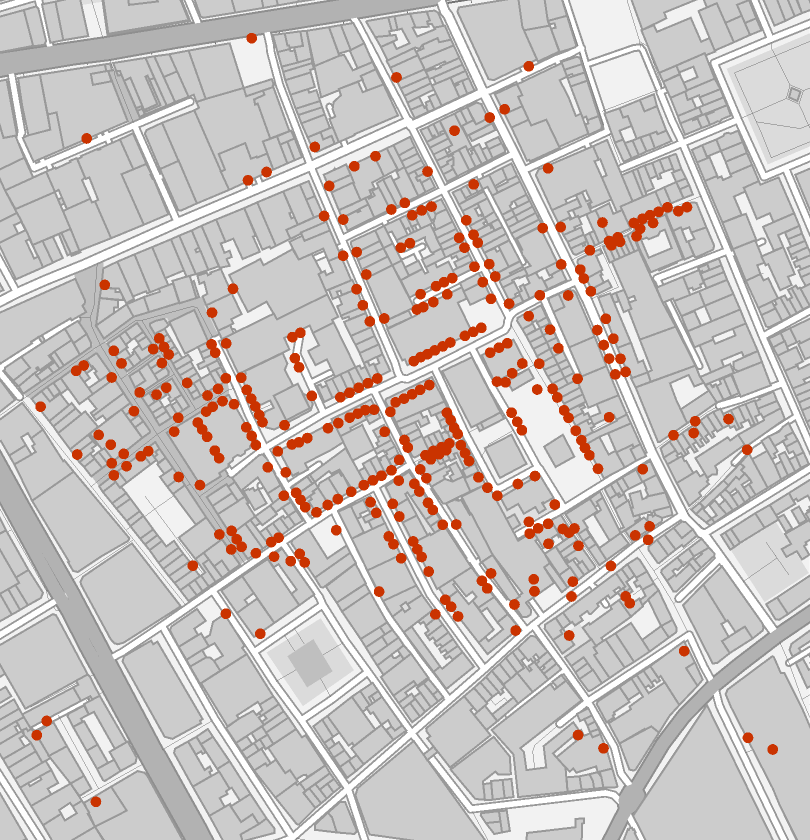

Visualize the number of cases per location with information whether the contaminated pump was the closest:

In[4]:=
legend = With[{cases = Union[ResourceData[\!\(\* TagBox["\"\<Sample Data: London Cholera\>\"", #& , BoxID -> "ResourceTag-Sample Data: London Cholera-Input", AutoDelete->True]\), "Data"][{"Annotations", "Cases"}][[1]]]}, PointLegend[ColorData[97, "ColorList"][[1 ;; Length[cases]]], cases, LegendLabel -> "number of cases \n per location", LegendMarkerSize -> 20, LegendFunction -> Frame]];
In[5]:=
Legended[PointValuePlot[ResourceData[\!\(\* TagBox["\"\<Sample Data: London Cholera\>\"", #& , BoxID -> "ResourceTag-Sample Data: London Cholera-Input", AutoDelete->True]\), "Data"], {1 -> Automatic, 2 -> None, 3 -> None, 4 -> None}, GeoBackground -> "VectorMonochrome"], legend]
Out[5]=

Analysis (4) 

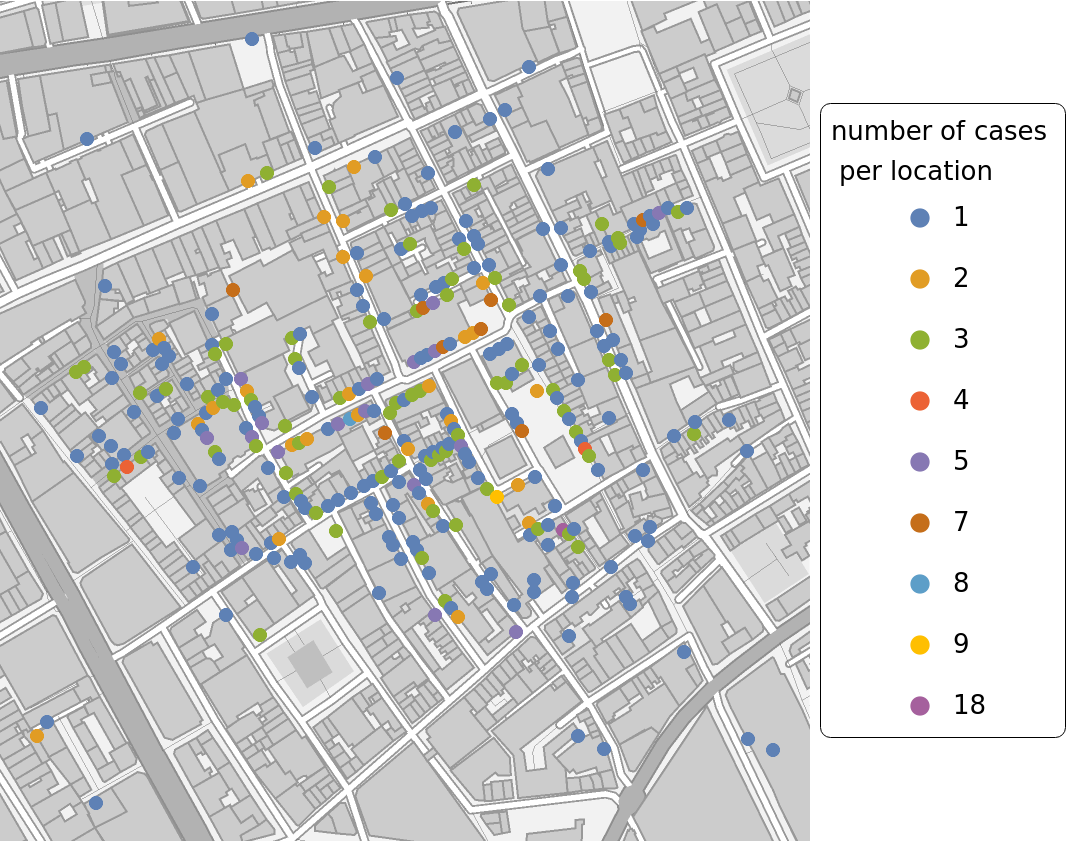Compute probability of finding a point within given radius of an existing point - NearestNeighborG is the CDF of the nearest neighbor distribution:

In[6]:=
nnG = NearestNeighborG[ResourceData[\!\(\* TagBox["\"\<Sample Data: London Cholera\>\"", #& , BoxID -> "ResourceTag-Sample Data: London Cholera-Input", AutoDelete->True]\), "Data"]]
Out[6]=
In[7]:=
maxRadius = nnG["MaxRadius"]
Out[7]=
In[8]:=
maxR = QuantityMagnitude[maxRadius, "km"]
Out[8]=
In[9]:=
DiscretePlot[ nnG[Quantity[r, "Kilometers"]], {r, maxR/100, maxR, maxR/100}, AxesLabel -> {"radius", "probability"}]
Out[9]=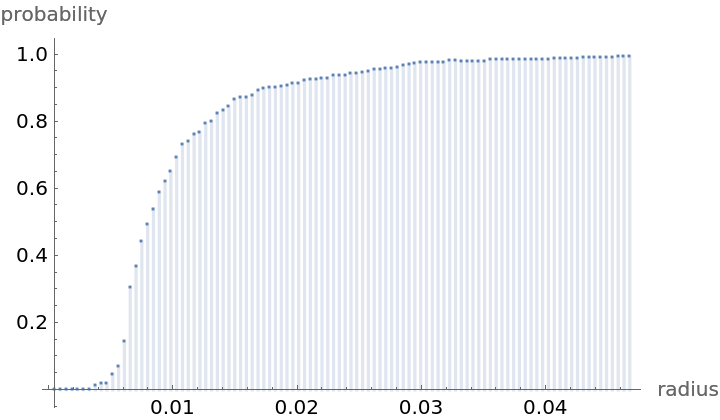

NearestNeighborG as the CDF of nearest neighbor distribution can be used to compute the mean distance between a typical point and its nearest neighbor - the mean of a positive support distribution can be approximated via a Riemann sum of 1- CDF. To use Riemann approximation create the partition of the support interval from 0 to maxR into 100 parts and compute the value of the NearestNeighborG at the middle of each subinterval:

In[10]:=
step = maxR/100; middles = Subdivide[step/2, maxR - step/2, 99]; values = nnG[middles];

Now compute the Riemann sum to find the mean distance between a typical point and its nearest neighbor:

In[11]:=
Quantity[Total[(1 - values)*step], "km"]
Out[11]=

Test for complete spacial randomness:

In[12]:=
SpatialRandomnessTest[ResourceData[\!\(\* TagBox["\"\<Sample Data: London Cholera\>\"", #& , BoxID -> "ResourceTag-Sample Data: London Cholera-Input", AutoDelete->True]\), "Data"], {"PValue", "TestConclusion"}]
Out[12]=

Gosia Konwerska, "Sample Data: London Cholera" from the Wolfram Data Repository (2022)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • Bivand, R.S., Pebesma, E., and Gomez-Rubio, V. (2013). Applied Spatial Data Analysis with R. New York, NY: Springer

Publisher Information

  • Prepared for the Wolfram Data Repository By: Gosia Konwerska
    (Wolfram Research, Inc.)
  • Publisher of Record: Gosia Konwerska