Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Sample Data: Ozarks Karst

Source Notebook

Locations of springs and sinkholes in the Ozark Plateaus Physiographic Province (Ozarks) in Arkansas

Details

Locations of springs and sinkholes in the Ozark Plateaus Physiographic Province (Ozarks) in Arkansas.

Examples

Basic Examples (2) 

Retrieve the data:

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Sample Data: Ozarks Karst\>\"", #& , BoxID -> "ResourceTag-Sample Data: Ozarks Karst-Input", AutoDelete->True]\), "Data"]
Out[1]=

Summary of the spatial point data:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<Sample Data: Ozarks Karst\>\"", #& , BoxID -> "ResourceTag-Sample Data: Ozarks Karst-Input", AutoDelete->True]\), "Data"]["Summary"]
Out[2]=

Visualizations (2) 

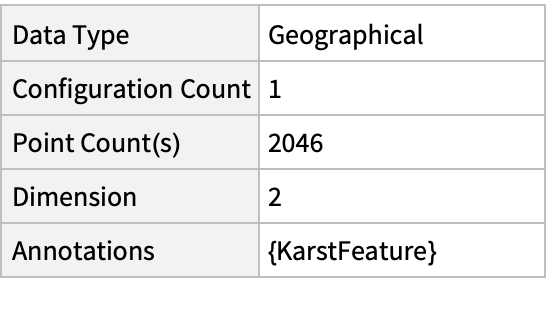Plot the spatial point data:

In[3]:=
GeoListPlot[ResourceData[\!\(\* TagBox["\"\<Sample Data: Ozarks Karst\>\"", #& , BoxID -> "ResourceTag-Sample Data: Ozarks Karst-Input", AutoDelete->True]\), "Data"]]
Out[3]=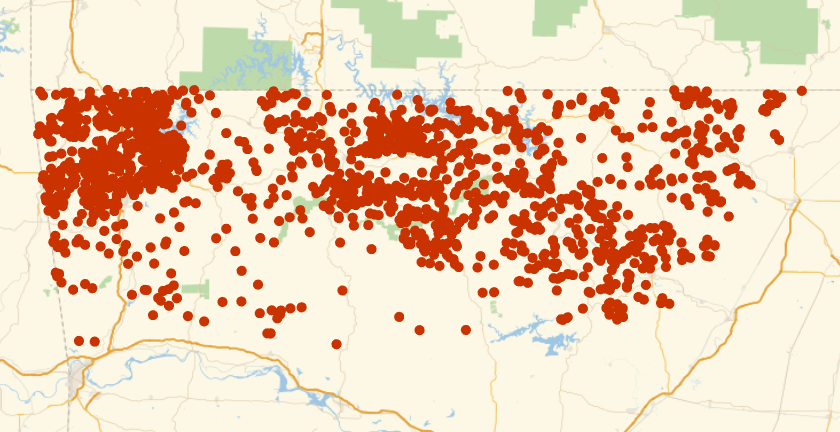

Visualize the data with annotations:

In[4]:=
legend = PointLegend[{Black, Orange}, {"sinkhole", "spring"}]; Legended[PointValuePlot[ResourceData[\!\(\* TagBox["\"\<Sample Data: Ozarks Karst\>\"", #& , BoxID -> "ResourceTag-Sample Data: Ozarks Karst-Input", AutoDelete->True]\), "Data"], PlotStyle -> {Black, Orange}], legend]
Out[5]=

Analysis (3) 

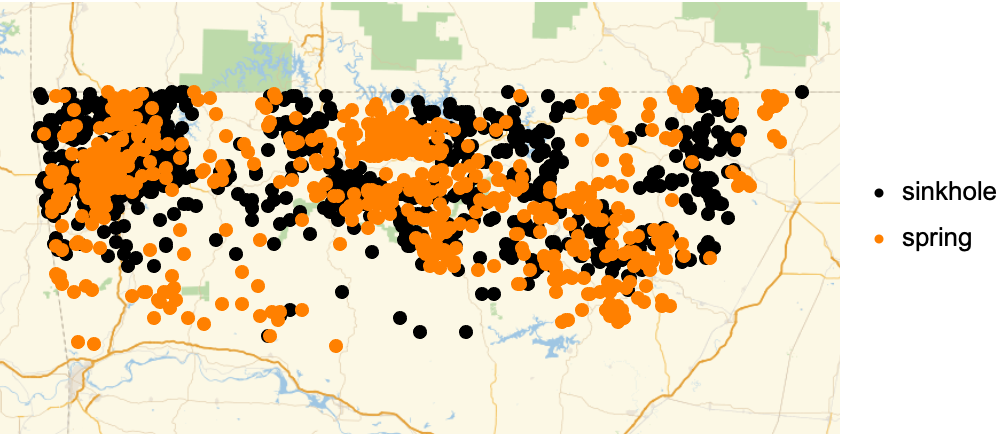Compute probability of finding a point within given radius of an existing point - NearestNeighborG is the CDF of the nearest neighbor distribution:

In[6]:=
nnG = NearestNeighborG[ResourceData[\!\(\* TagBox["\"\<Sample Data: Ozarks Karst\>\"", #& , BoxID -> "ResourceTag-Sample Data: Ozarks Karst-Input", AutoDelete->True]\), "Data"]]
Out[6]=
In[7]:=
maxR = nnG["MaxRadius"]
Out[7]=
In[8]:=
res = nnG[r = Range[Quantity[0, "Miles"], maxR, maxR/20]];
In[9]:=
ListPlot[Transpose[{r, res}], AxesLabel -> {"radius", "probability"}, Filling -> Axis]
Out[9]=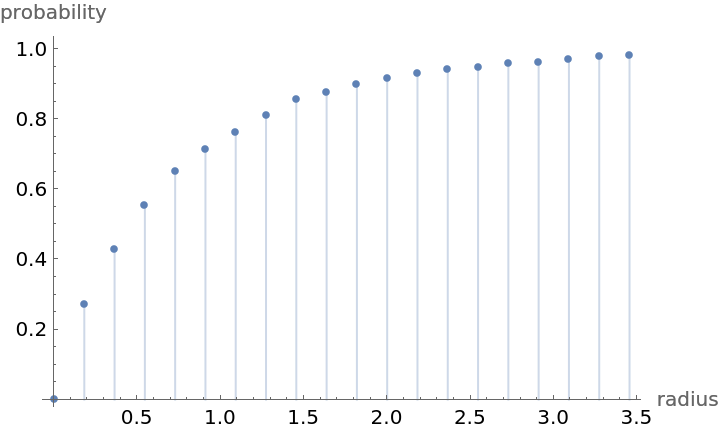

Mean distance between a typical point and its nearest neighbor (for positive support distribution can be approximated via a Riemann sum of 1-CDF):

In[10]:=
step = maxR/100; partition = Table[{k, k + step}, {k, 0, maxR, step}]; values = nnG[Mean /@ partition];
In[11]:=
Total[(1 - values)*step]
Out[11]=

Test for complete spatial randomness:

In[12]:=
SpatialRandomnessTest[ResourceData[\!\(\* TagBox["\"\<Sample Data: Ozarks Karst\>\"", #& , BoxID -> "ResourceTag-Sample Data: Ozarks Karst-Input", AutoDelete->True]\), "Data"], {"PValue", "TestConclusion"}] // Column
Out[12]=

Gosia Konwerska, "Sample Data: Ozarks Karst" from the Wolfram Data Repository (2021)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation: https://www.sciencebase.gov/catalog/item/5728fd86e4b0b13d3918aa3e

Publisher Information

  • Prepared for the Wolfram Data Repository By: Gosia Konwerska
    (Wolfram Research, Inc.)
  • Publisher of Record: Gosia Konwerska