Wolfram Data Repository
Immediate Computable Access to Curated Contributed Data
Locations of people in Gordon Square without annotations
| In[1]:= |
| Out[1]= | 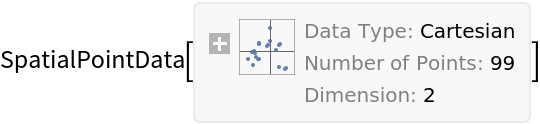 |
Summary of the spatial point data:
| In[2]:= |
| Out[2]= | 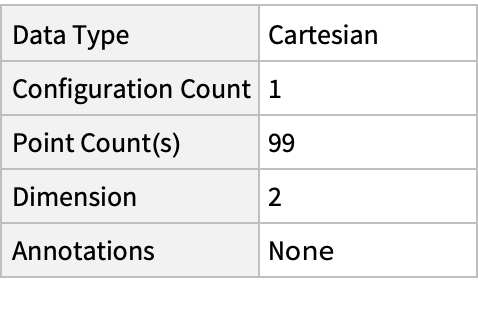 |
Plot the spatial point data:
| In[3]:= |
| Out[3]= | 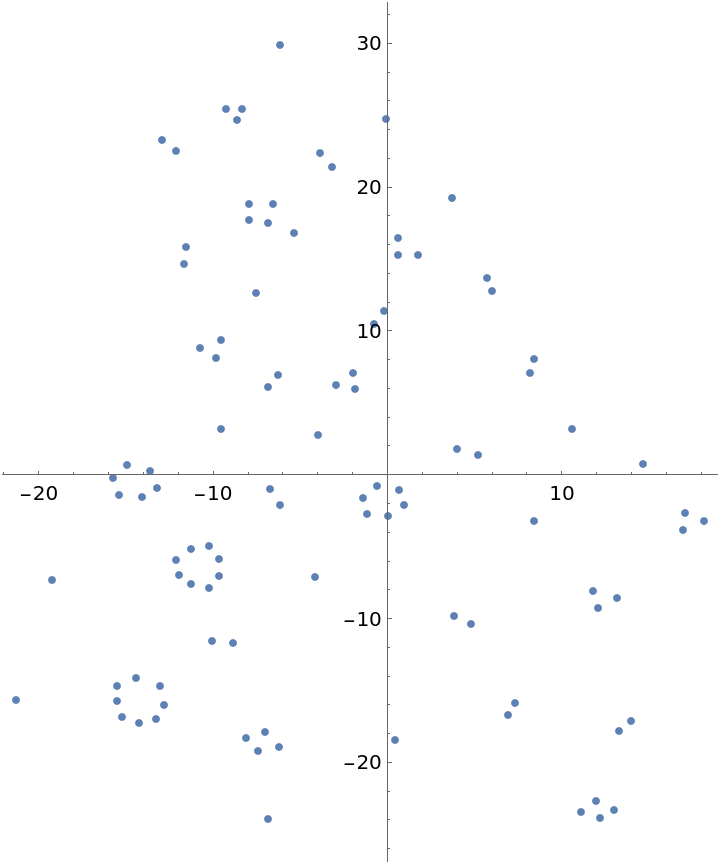 |
Visualize data within observation region and bounding rectangle:
| In[4]:= | ![Graphics[{Opacity[.1], Rectangle[{-26.4085, -36.3209}, {26.4085, 36.3209}], Darker@Green, Opacity[.5], ResourceData[\!\(\*
TagBox["\"\<Sample Data: People In Gordon Square\>\"",
#& ,
BoxID -> "ResourceTag-Sample Data: People In Gordon Square-Input",
AutoDelete->True]\), "ObservationRegion"], Black, Opacity[1], Point[ResourceData[\!\(\*
TagBox["\"\<Sample Data: People In Gordon Square\>\"",
#& ,
BoxID -> "ResourceTag-Sample Data: People In Gordon Square-Input",
AutoDelete->True]\), "Locations"]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/532/5327411d-19fb-4ee0-bc76-78d64dfe734c/40ceaa61ddda3895.png) |
| Out[4]= |  |
Plot the smooth point density:
| In[5]:= |
| Out[5]= |  |
| In[6]:= | ![Show[ContourPlot[density[{x, y}], {x, y} \[Element] ResourceData[\!\(\*
TagBox["\"\<Sample Data: People In Gordon Square\>\"",
#& ,
BoxID -> "ResourceTag-Sample Data: People In Gordon Square-Input",
AutoDelete->True]\), "ObservationRegion"], ColorFunction -> "Rainbow"], ListPlot[ResourceData[\!\(\*
TagBox["\"\<Sample Data: People In Gordon Square\>\"",
#& ,
BoxID -> "ResourceTag-Sample Data: People In Gordon Square-Input",
AutoDelete->True]\), "Data"], PlotStyle -> Black]]](https://www.wolframcloud.com/obj/resourcesystem/images/532/5327411d-19fb-4ee0-bc76-78d64dfe734c/1d5eb231ccb80263.png) |
| Out[6]= | 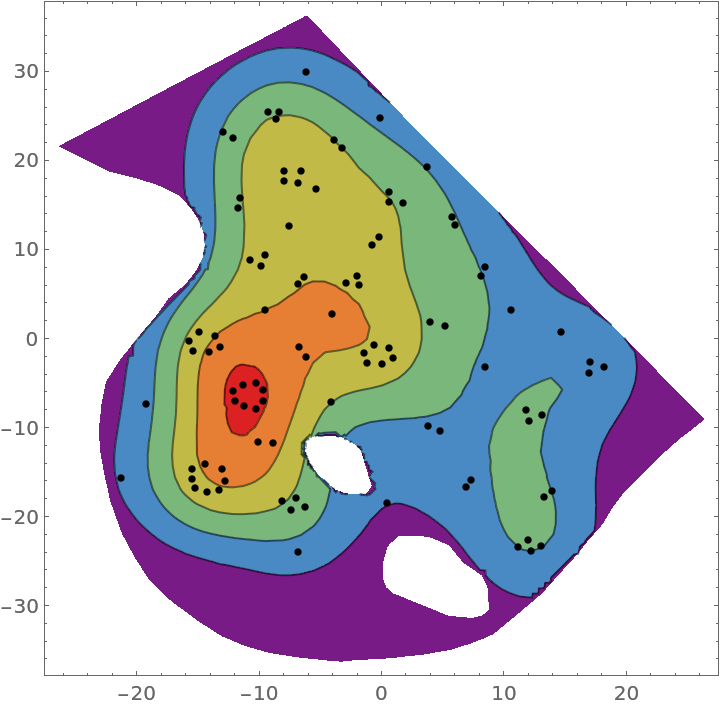 |
Compute probability of finding a point within given radius of an existing point - NearestNeighborG is the CDF of the nearest neighbor distribution:
| In[7]:= |
| Out[7]= |  |
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= | 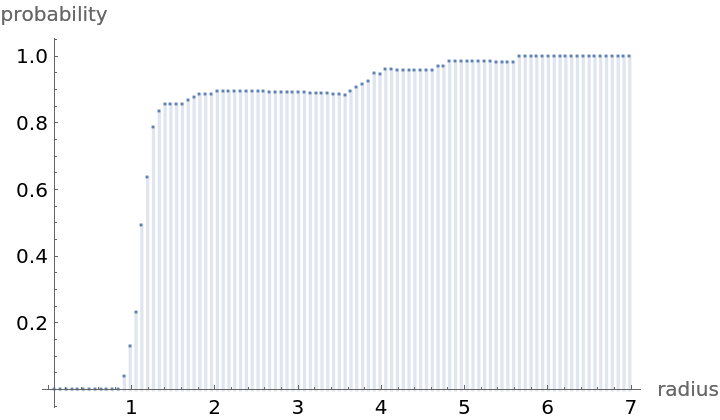 |
NearestNeighborG as the CDF of nearest neighbor distribution can be used to compute the mean distance between a typical point and its nearest neighbor - the mean of a positive support distribution can be approximated via a Riemann sum of 1- CDF. To use Riemann approximation create the partition of the support interval from 0 to maxR into 100 parts and compute the value of the NearestNeighborG at the middle of each subinterval:
| In[10]:= | ![step = maxR/100;
middles = Subdivide[step/2, maxR - step/2, 99];
values = nnG[middles];](https://www.wolframcloud.com/obj/resourcesystem/images/532/5327411d-19fb-4ee0-bc76-78d64dfe734c/53014afd82ea866b.png) |
Now compute the Riemann sum to find the mean distance between a typical point and its nearest neighbor:
| In[11]:= |
| Out[11]= |
Account for scale and units:
| In[12]:= |
| Out[12]= |
Test for complete spacial randomness:
| In[13]:= |
| Out[13]= |  |
Fit a hardcore point process to data:
| In[14]:= | ![Clear[\[Mu], r];
EstimatedPointProcess[ResourceData[\!\(\*
TagBox["\"\<Sample Data: People In Gordon Square\>\"",
#& ,
BoxID -> "ResourceTag-Sample Data: People In Gordon Square-Input",
AutoDelete->True]\), "Data"], HardcorePointProcess[\[Mu], r, 2]]](https://www.wolframcloud.com/obj/resourcesystem/images/532/5327411d-19fb-4ee0-bc76-78d64dfe734c/4db2ffcde9faa058.png) |
| Out[15]= |
Gosia Konwerska, "Sample Data: People In Gordon Square" from the Wolfram Data Repository (2022)