Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Sample Data: Scallop Abundance

Source Notebook

Locations of scallop samples in the Atlantic Ocean, annotated with the numbers and types of scallops caught

Details

Locations of scallop samples in the Atlantic Ocean in the observation region which is the convex hull of the sample locations, annotated with marks including the total number of scallops caught, the number of pre-recruit scallops (<70mm shell length), and the number of recruit scallops (>=70mm shell length).

Examples

Basic Examples (1) 

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Sample Data: Scallop Abundance\>\"", #& , BoxID -> "ResourceTag-Sample Data: Scallop Abundance-Input", AutoDelete->True]\), "Data"]
Out[1]=

Summary of the spatial point data:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<Sample Data: Scallop Abundance\>\"", #& , BoxID -> "ResourceTag-Sample Data: Scallop Abundance-Input", AutoDelete->True]\), "Data"]["Summary"]
Out[2]=

Visualizations (3) 

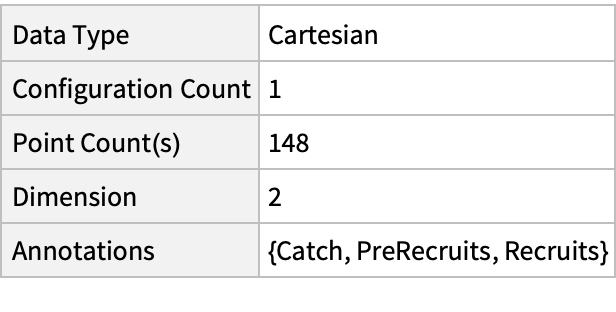Plot the spatial point data:

In[3]:=
ListPlot[ResourceData[\!\(\* TagBox["\"\<Sample Data: Scallop Abundance\>\"", #& , BoxID -> "ResourceTag-Sample Data: Scallop Abundance-Input", AutoDelete->True]\), "Data"], AspectRatio -> Full]
Out[3]=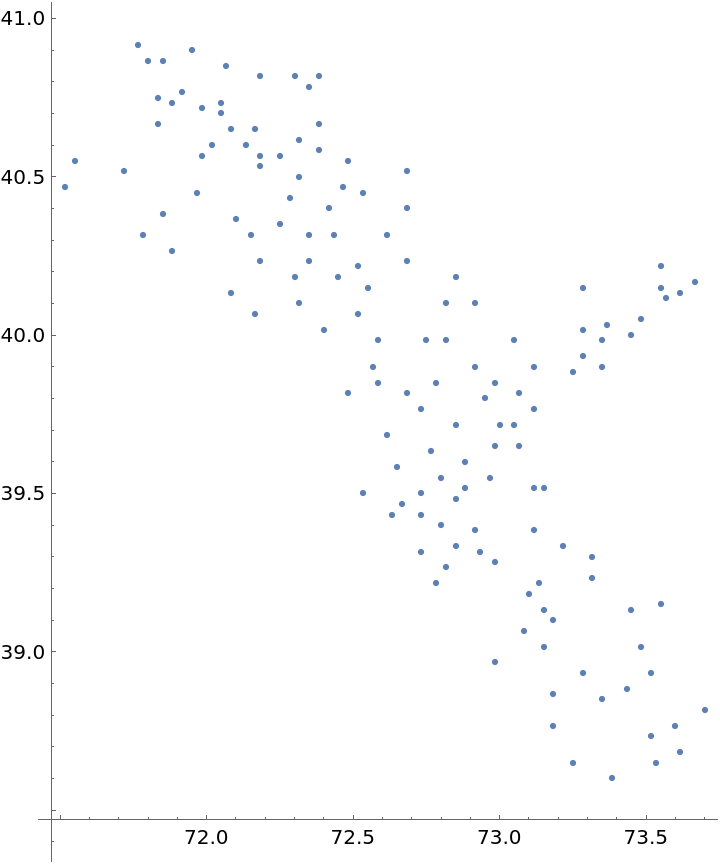

Visualize the data with some annotations:

In[4]:=
PointValuePlot[ResourceData[\!\(\* TagBox["\"\<Sample Data: Scallop Abundance\>\"", #& , BoxID -> "ResourceTag-Sample Data: Scallop Abundance-Input", AutoDelete->True]\), "Data"], {1 -> Automatic, 2 -> None, 3 -> None}, PlotLegends -> Automatic, PlotLabel -> "Catch"]
Out[4]=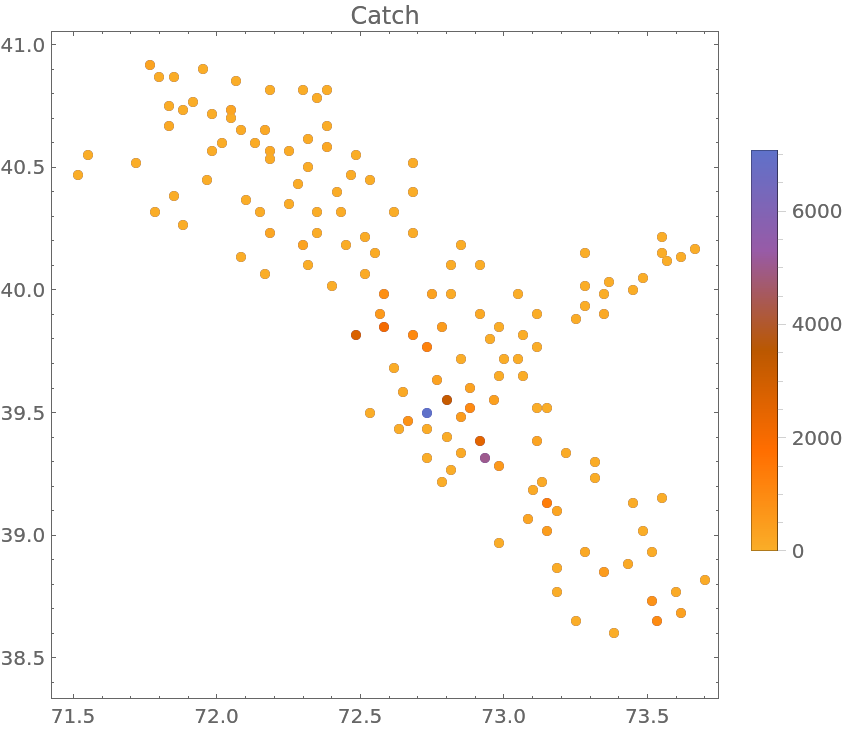

Visualize the smooth point density of the data:

In[5]:=
density = SmoothPointDensity[ResourceData[\!\(\* TagBox["\"\<Sample Data: Scallop Abundance\>\"", #& , BoxID -> "ResourceTag-Sample Data: Scallop Abundance-Input", AutoDelete->True]\), "Data"]]
Out[5]=
In[6]:=
Show[ContourPlot[density[{x, y}], {x, y} \[Element] ResourceData[\!\(\* TagBox["\"\<Sample Data: Scallop Abundance\>\"", #& , BoxID -> "ResourceTag-Sample Data: Scallop Abundance-Input", AutoDelete->True]\), "ObservationRegion"], ColorFunction -> "Rainbow"], ListPlot[ResourceData[\!\(\* TagBox["\"\<Sample Data: Scallop Abundance\>\"", #& , BoxID -> "ResourceTag-Sample Data: Scallop Abundance-Input", AutoDelete->True]\), "Data"], PlotStyle -> Black]]
Out[6]=

Analysis (5) 

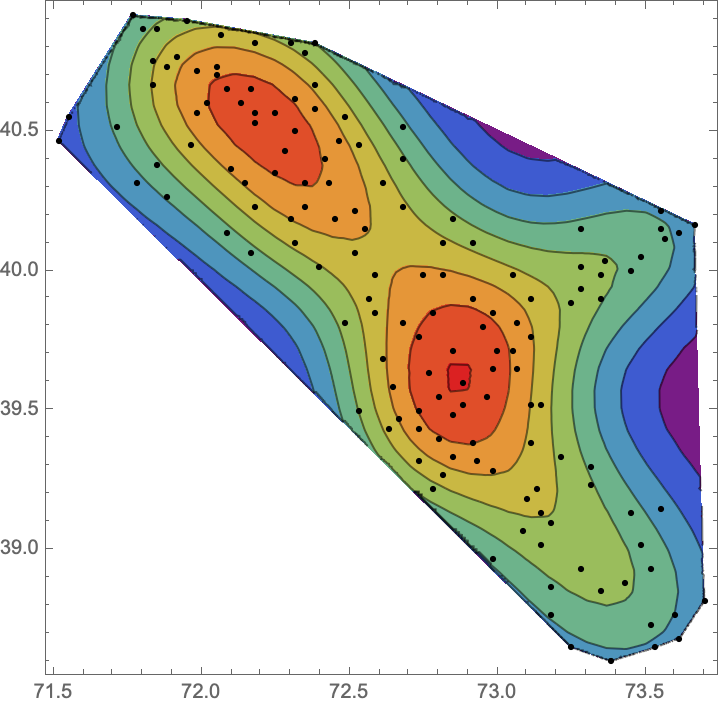Use SpatialEstimate to create an estimate of recruit percentage from sparse catch locations. First select locations with positive catch numbers:

In[7]:=
pos = Position[ResourceData[\!\(\* TagBox["\"\<Sample Data: Scallop Abundance\>\"", #& , BoxID -> "ResourceTag-Sample Data: Scallop Abundance-Input", AutoDelete->True]\), "Annotations"]["Catch"], _?Positive];
In[8]:=
locs = Extract[ResourceData[\!\(\* TagBox["\"\<Sample Data: Scallop Abundance\>\"", #& , BoxID -> "ResourceTag-Sample Data: Scallop Abundance-Input", AutoDelete->True]\), "Locations"], pos];

Compute rate of recruits relative to the catch size:

In[9]:=
recruitsRate = Extract[ResourceData[\!\(\* TagBox["\"\<Sample Data: Scallop Abundance\>\"", #& , BoxID -> "ResourceTag-Sample Data: Scallop Abundance-Input", AutoDelete->True]\), "Annotations"]["Recruits"], pos]/ Extract[ResourceData[\!\(\* TagBox["\"\<Sample Data: Scallop Abundance\>\"", #& , BoxID -> "ResourceTag-Sample Data: Scallop Abundance-Input", AutoDelete->True]\), "Annotations"]["Catch"], pos] // N;

Compute spatial prediction:

In[10]:=
est = SpatialEstimate[locs -> recruitsRate, VariogramFunction -> "Gaussian"]
Out[10]=
Create a set of random points and compute the estimated values at these locations:
In[11]:=
pts = RandomPoint[ResourceData[\!\(\* TagBox["\"\<Sample Data: Scallop Abundance\>\"", #& , BoxID -> "ResourceTag-Sample Data: Scallop Abundance-Input", AutoDelete->True]\), "ObservationRegion"], 1000]; vals = est[pts];

Visualize the recruits rates over the whole observation region:

In[12]:=
Row@{PointValuePlot[locs -> recruitsRate, ColorFunction -> "Rainbow", PlotLegends -> Automatic, PlotLabel -> "recruits rates"], PointValuePlot[pts -> vals, PlotStyle -> PointSize[Medium], ColorFunction -> "Rainbow", PlotLabel -> "estimated recruits rates"]}
Out[12]=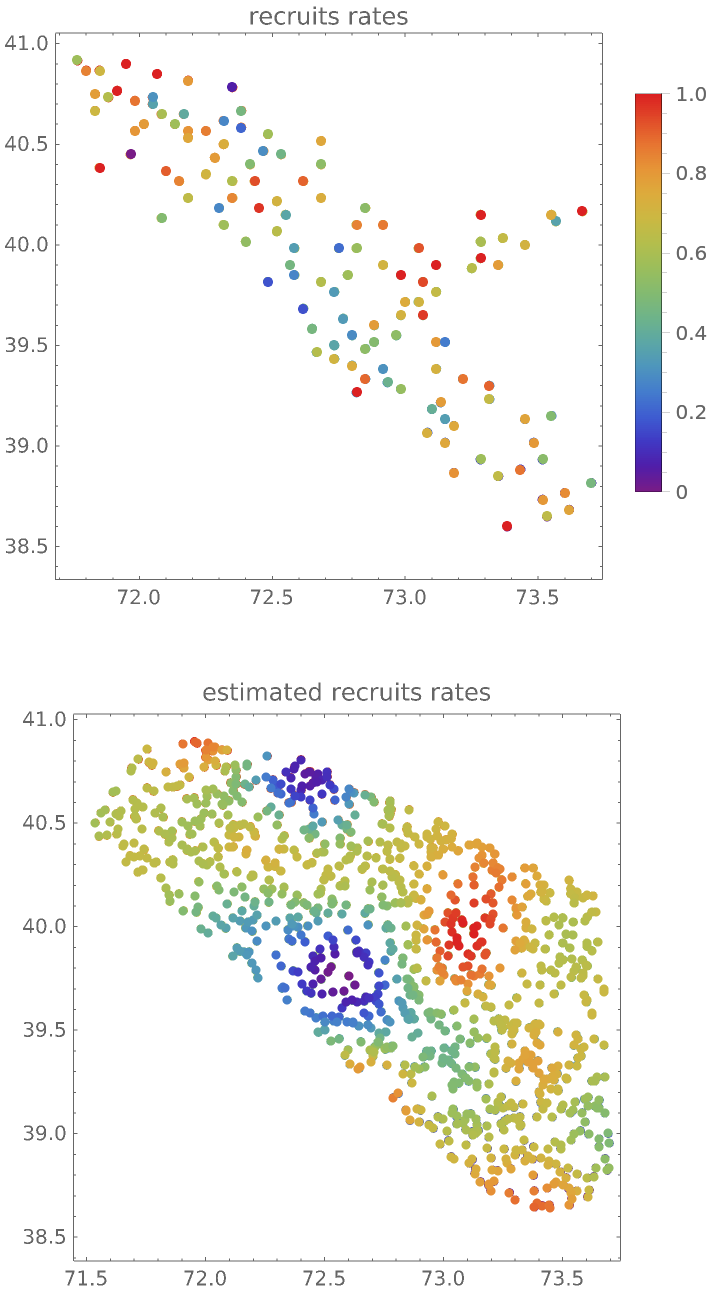

Gosia Konwerska, "Sample Data: Scallop Abundance" from the Wolfram Data Repository (2022)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation: Ecker, M. D. and Heltshe, J. F. (1994). Case Studies in Biometry. Wiley, New Jersey.

Publisher Information

  • Prepared for the Wolfram Data Repository By: Gosia Konwerska
    (Wolfram Research, Inc.)
  • Publisher of Record: Gosia Konwerska