Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Sample Data: Spruce Trees

Source Notebook

Locations of spruce trees annotated with diameter marks

Details

Locations of spruce trees in the observation region Rectangle[{0, 0}, {56, 38}] meters, annotated with diameter marks.

Examples

Basic Examples (1) 

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Sample Data: Spruce Trees\>\"", #& , BoxID -> "ResourceTag-Sample Data: Spruce Trees-Input", AutoDelete->True]\), "Data"]
Out[1]=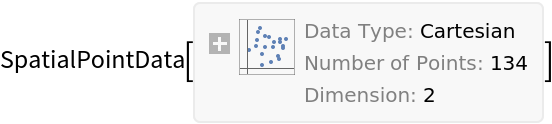

Summary of the spatial point data:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<Sample Data: Spruce Trees\>\"", #& , BoxID -> "ResourceTag-Sample Data: Spruce Trees-Input", AutoDelete->True]\), "Data"]["Summary"]
Out[2]=

Visualizations (3) 

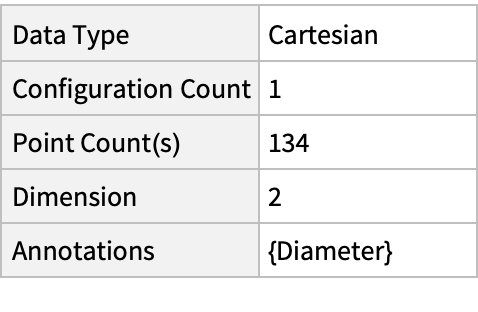Plot the spatial point data:

In[3]:=
ListPlot[ResourceData[\!\(\* TagBox["\"\<Sample Data: Spruce Trees\>\"", #& , BoxID -> "ResourceTag-Sample Data: Spruce Trees-Input", AutoDelete->True]\), "Data"]]
Out[3]=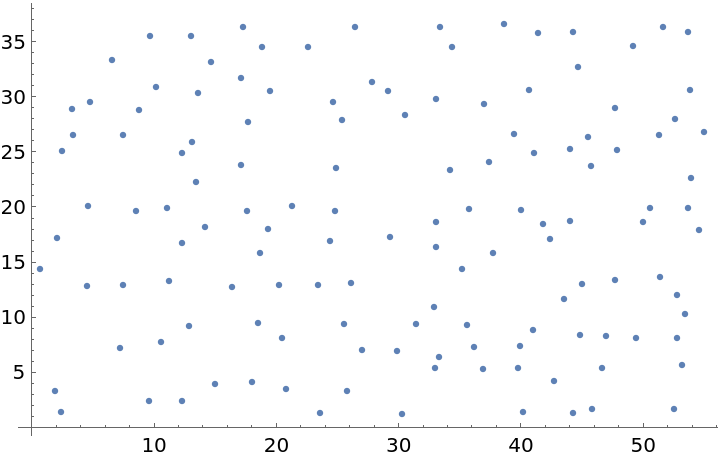

Visualize point with annotations:

In[4]:=
PointValuePlot[ResourceData[\!\(\* TagBox["\"\<Sample Data: Spruce Trees\>\"", #& , BoxID -> "ResourceTag-Sample Data: Spruce Trees-Input", AutoDelete->True]\), "Data"], {1 -> "Size"}]
Out[4]=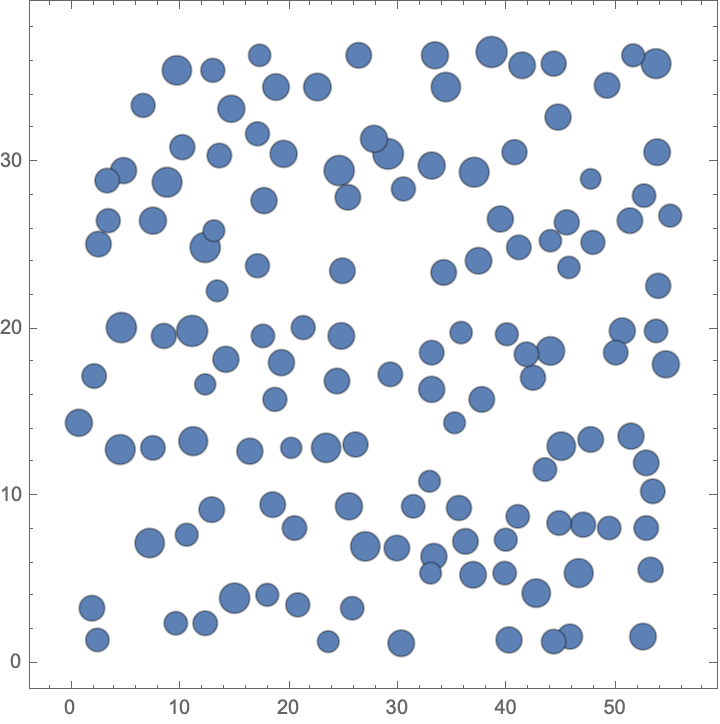

Visualize smooth point density:

In[5]:=
density = SmoothPointDensity[ResourceData[\!\(\* TagBox["\"\<Sample Data: Spruce Trees\>\"", #& , BoxID -> "ResourceTag-Sample Data: Spruce Trees-Input", AutoDelete->True]\), "Data"]]
Out[5]=
In[6]:=
Show[ContourPlot[density[{x, y}], {x, y} \[Element] ResourceData[\!\(\* TagBox["\"\<Sample Data: Spruce Trees\>\"", #& , BoxID -> "ResourceTag-Sample Data: Spruce Trees-Input", AutoDelete->True]\), "ObservationRegion"], ColorFunction -> "Rainbow"], ListPlot[ResourceData[\!\(\* TagBox["\"\<Sample Data: Spruce Trees\>\"", #& , BoxID -> "ResourceTag-Sample Data: Spruce Trees-Input", AutoDelete->True]\), "Data"], PlotStyle -> Black]]
Out[6]=

Analysis (6) 

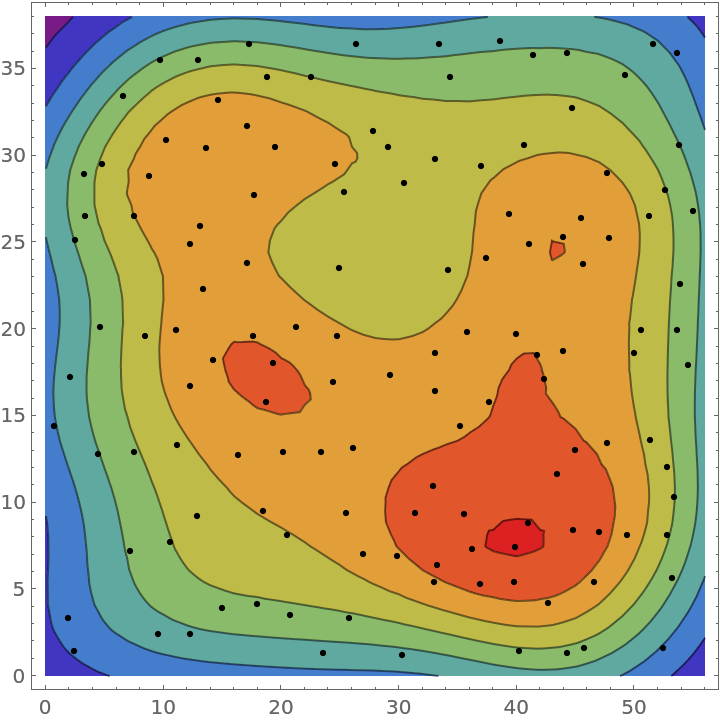Compute probability of finding a point within given radius of an existing point - NearestNeighborG is the CDF of the nearest neighbor distribution:

In[7]:=
nnG = NearestNeighborG[ResourceData[\!\(\* TagBox["\"\<Sample Data: Spruce Trees\>\"", #& , BoxID -> "ResourceTag-Sample Data: Spruce Trees-Input", AutoDelete->True]\), "Data"]]
Out[7]=
In[8]:=
maxR = nnG["MaxRadius"]
Out[8]=
In[9]:=
DiscretePlot[nnG[r], {r, maxR/100, maxR, maxR/100}, AxesLabel -> {"radius", "probability"}]
Out[9]=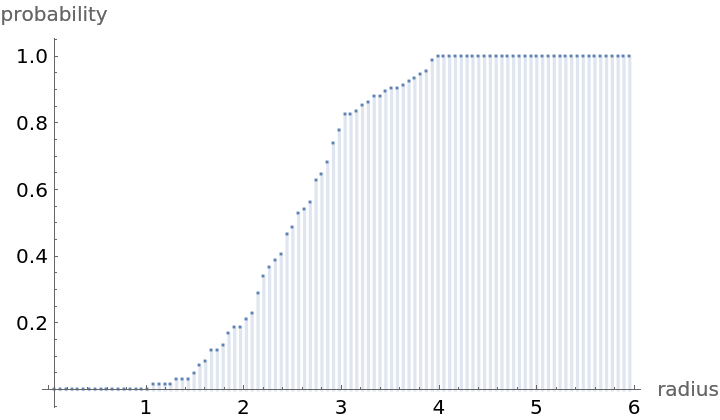

NearestNeighborG as the CDF of nearest neighbor distribution can be used to compute the mean distance between a typical point and its nearest neighbor - the mean of a positive support distribution can be approximated via a Riemann sum of 1- CDF. To use Riemann approximation create the partition of the support interval from 0 to maxR into 100 parts and compute the value of the NearestNeighborG at the middle of each subinterval:

In[10]:=
step = maxR/100; middles = Subdivide[step/2, maxR - step/2, 99]; values = nnG[middles];

Now compute the Riemann sum to find the mean distance between a typical point and its nearest neighbor:

In[11]:=
Total[(1 - values)*step]
Out[11]=

Account for scale and units:

In[12]:=
%*ResourceData[\!\(\* TagBox["\"\<Sample Data: Spruce Trees\>\"", #& , BoxID -> "ResourceTag-Sample Data: Spruce Trees-Input", AutoDelete->True]\), "RegionScale"]
Out[12]=

Test for complete spacial randomness:

In[13]:=
SpatialRandomnessTest[ResourceData[\!\(\* TagBox["\"\<Sample Data: Spruce Trees\>\"", #& , BoxID -> "ResourceTag-Sample Data: Spruce Trees-Input", AutoDelete->True]\), "Data"], {"PValue", "TestConclusion"}] // Column
Out[13]=

Fit a Poisson point process to data:

In[14]:=
Clear[\[Mu]]; EstimatedPointProcess[ResourceData[\!\(\* TagBox["\"\<Sample Data: Spruce Trees\>\"", #& , BoxID -> "ResourceTag-Sample Data: Spruce Trees-Input", AutoDelete->True]\), "Data"], PoissonPointProcess[\[Mu], 2]]
Out[15]=

Gosia Konwerska, "Sample Data: Spruce Trees" from the Wolfram Data Repository (2022)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • Stoyan D., Kendall W., Mecke J., (1987). Stochastic Geometry and its Applications. John Wiley and Sons, Chichester.

Publisher Information

  • Prepared for the Wolfram Data Repository By: Gosia Konwerska
    (Wolfram Research, Inc.)
  • Publisher of Record: Gosia Konwerska