Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

The Busy Beaver Competition

Source Notebook

Current Busy Beaver Records, winning Turing Machines and references

Details

There are (2k n+1)k n Turing machines with k states and n symbols. Each of them can be launched on a blank tape, that is a tape with symbols 0 in all cells. Then some of them never stop, and the other ones eventually stop. Those which stop are called busy beavers.
Busy beavers compete in two competitions: - to take the most time to stop - to leave the most non-blank symbols on the tape when stopping
Record holders are named by their k,n index, if the record changes, old one gets renamed to k,n.i with i starting from 0.

(1 entity types, 1 entities, 1 properties)

Examples

Basic Examples (3) 

In[1]:=
ResourceData["The Busy Beaver Competition"]
Out[1]=

Register the EntityStore:

In[2]:=
EntityRegister[ResourceData["The Busy Beaver Competition"]]
Out[2]=

Make a dataset with Busy Beaver record Turing machines:

In[3]:=
EntityValue["BusyBeaverRecords", "Dataset"][[;; 3]]
Out[3]=

Visualizations (4) 

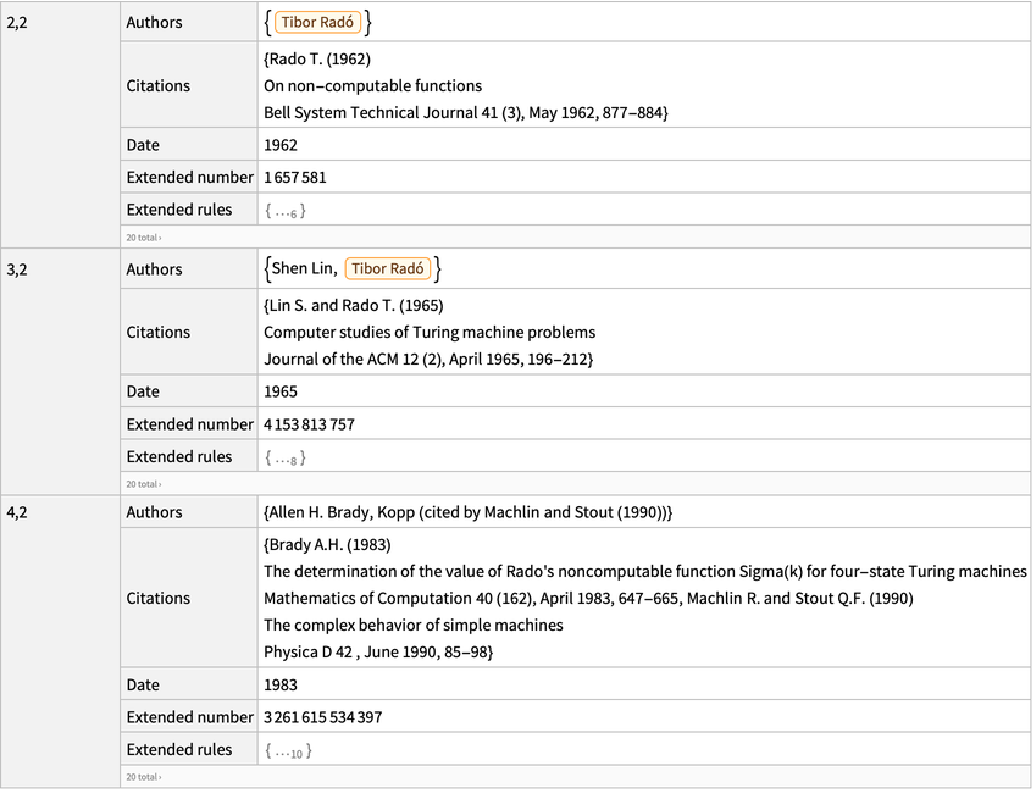Make a summary table of all records:

In[4]:=
Text@Grid[{{Style["s", Italic], Style["k", Italic], "number", "lifetime"}, Splice@EntityValue[ EntityList[ FilteredEntityClass["BusyBeaverRecords", EntityFunction[e, e["Winner"]]]], {"StateCount", "SymbolCount", "RuleCount", "S"}]}, Frame -> All, FrameStyle -> GrayLevel[0, .2], Dividers -> {All, {7 -> Thick}}, Spacings -> {1, .6}, Background -> {White, {GrayLevel[.85]}}]
Out[4]=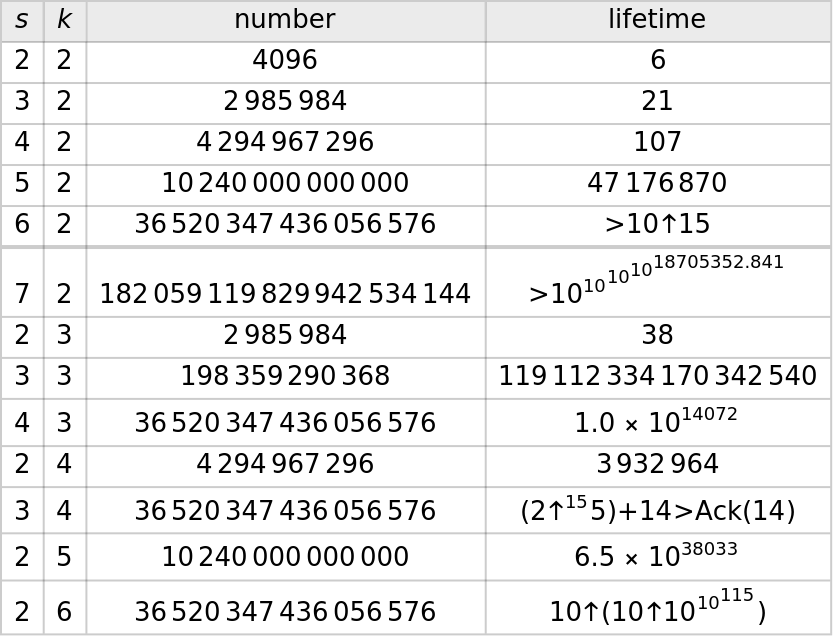

Show the timeline of records for different machine signatures and their authors:

In[5]:=
TimelinePlot[ EntityValue[#, "Date"] -> Row[{#, Row[EntityValue[#, "Authors"], ","]}] & /@ EntityList["BusyBeaverRecords"]]
Out[5]=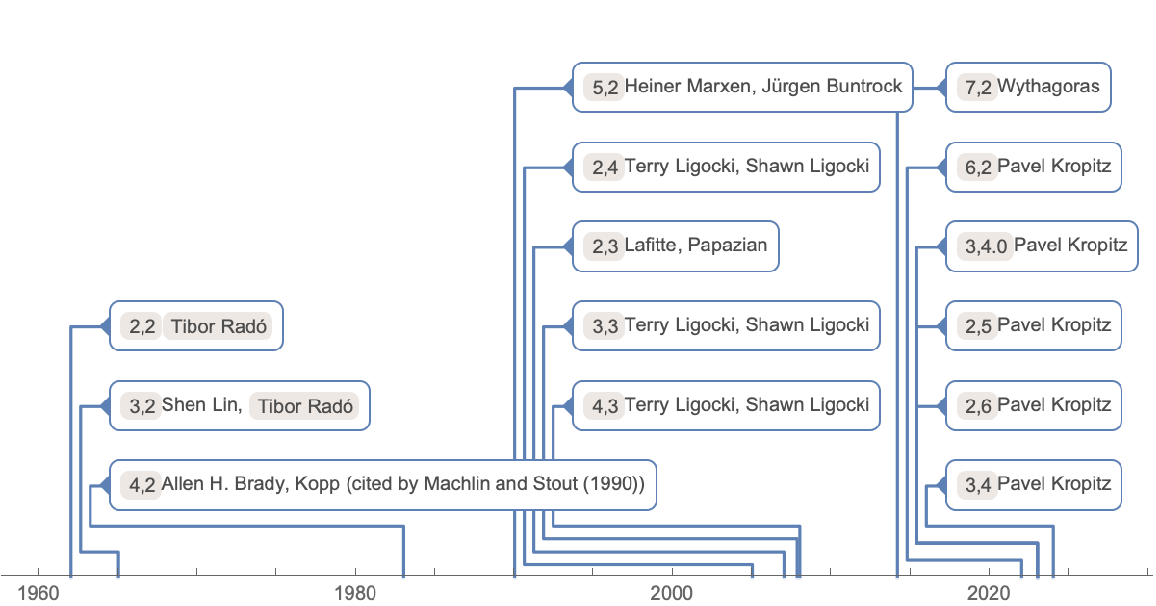

Show evolutions of small Busy Beaver Turing machines up-to their halting time:

In[6]:=
RulePlot[ TuringMachine[ EntityValue[Entity["BusyBeaverRecords", #], "Rules"]], {1, {{}, 0}}, EntityValue[Entity["BusyBeaverRecords", #], "S"]] & /@ {"2,2", "3,2", "4,2", "2,3"}
Out[6]=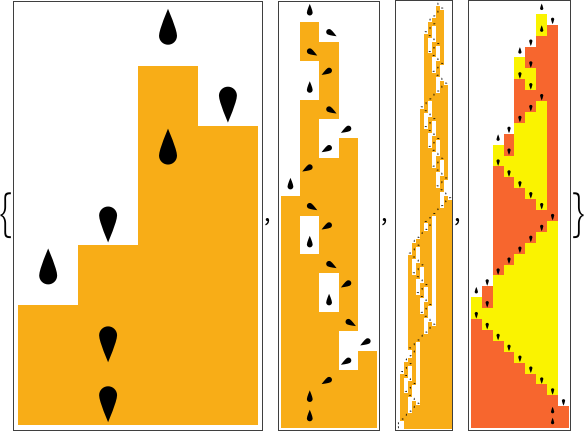

Show last tape configurations of the record 2,4 machine:

In[7]:=
evolution = TuringMachine[ EntityValue[Entity["BusyBeaverRecords", "2,4"], "Rules"], {1, {{}, 0}}, EntityValue[Entity["BusyBeaverRecords", "2,4"], "S"] + 5 ]; // AbsoluteTiming
Out[7]=
In[8]:=
RulePlot[TuringMachine[ EntityValue[Entity["BusyBeaverRecords", "2,4"], "Rules"]], evolution[[-1000 ;;]]]
Out[8]=

Prove that the machine terminates by confirming that the last two configurations are the same:

In[9]:=
Equal @@ evolution[[-2 ;;, 2]]
Out[9]=

Wolfram Research, "The Busy Beaver Competition" from the Wolfram Data Repository (2024)  

Data Resource History

  • Date Created:

Source Metadata

  • Title: The Busy Beaver Competitions
  • Creator: Pascal Michel
  • Date: 2023
  • Citation: Source, reference or citation information

See Also

Publisher Information

  • Prepared for the Wolfram Data Repository By: Nik Murzin
  • Publisher of Record: Wolfram Research