Wolfram Research

Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Theorem Network from Euclid's Elements

Source Notebook

Graph of interdependence of theorems from Euclid's Elements

Details

The nodes correspond to theorems, common notions and postulates.
Each node is a connected to nodes corresponding to the theorems etc. referenced in its proof.
A version of this network originally appeared in A New Kind of Science (Wolfram, 2002) on page 1176.

Examples

Basic Examples

Retrieve the basic network:

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Theorem Network from Euclid's Elements\>\"", #& , BoxID -> "ResourceTag-Theorem Network from Euclid's Elements-Input", AutoDelete->True]\)]
Out[1]=

Make a layered graph plot:

In[2]:=
LayeredGraphPlot[ResourceData[\!\(\* TagBox["\"\<Theorem Network from Euclid's Elements\>\"", #& , BoxID -> "ResourceTag-Theorem Network from Euclid's Elements-Input", AutoDelete->True]\)], AspectRatio -> 1/2]
Out[2]=

Find axioms and theorems referenced by Book 1, Theorem 5:

In[3]:=
VertexOutComponent[ResourceData[\!\(\* TagBox["\"\<Theorem Network from Euclid's Elements\>\"", #& , BoxID -> "ResourceTag-Theorem Network from Euclid's Elements-Input", AutoDelete->True]\)], <|"Book" -> 1, "Theorem" -> 5|>, 1]
Out[3]=

Analysis

Count the total number of theorems + axioms:

In[4]:=
VertexCount[ResourceData[\!\(\* TagBox["\"\<Theorem Network from Euclid's Elements\>\"", #& , BoxID -> "ResourceTag-Theorem Network from Euclid's Elements-Input", AutoDelete->True]\)]]
Out[4]=

Find the axioms:

In[5]:=
Select[VertexList[ResourceData[\!\(\* TagBox["\"\<Theorem Network from Euclid's Elements\>\"", #& , BoxID -> "ResourceTag-Theorem Network from Euclid's Elements-Input", AutoDelete->True]\)]], Length[#] < 2 &]
Out[5]=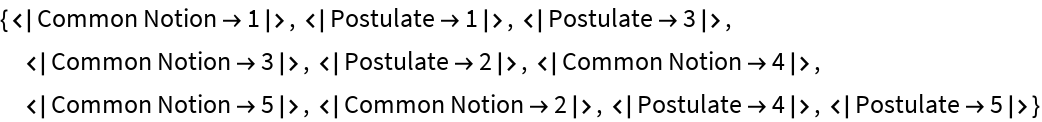

Find the distribution of numbers of theorems referenced:

In[6]:=
Histogram[VertexOutDegree[ResourceData[\!\(\* TagBox["\"\<Theorem Network from Euclid's Elements\>\"", #& , BoxID -> "ResourceTag-Theorem Network from Euclid's Elements-Input", AutoDelete->True]\)]]]
Out[6]=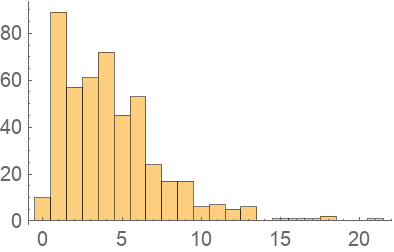

Find the 5 most referenced theorems:

In[7]:=
TakeLargestBy[VertexList[ResourceData[\!\(\* TagBox["\"\<Theorem Network from Euclid's Elements\>\"", #& , BoxID -> "ResourceTag-Theorem Network from Euclid's Elements-Input", AutoDelete->True]\)]], VertexInDegree[ResourceData[\!\(\* TagBox["\"\<Theorem Network from Euclid's Elements\>\"", #& , BoxID -> "ResourceTag-Theorem Network from Euclid's Elements-Input", AutoDelete->True]\)], #] &, 5]
Out[7]=

Find the total number of theorems + axioms that ultimately contribute to the proof of each theorem:

In[8]:=
ListLinePlot[Length[VertexOutComponent[ResourceData[\!\(\* TagBox["\"\<Theorem Network from Euclid's Elements\>\"", #& , BoxID -> "ResourceTag-Theorem Network from Euclid's Elements-Input", AutoDelete->True]\)], #]] & /@ VertexList[ResourceData[\!\(\* TagBox["\"\<Theorem Network from Euclid's Elements\>\"", #& , BoxID -> "ResourceTag-Theorem Network from Euclid's Elements-Input", AutoDelete->True]\)]]]
Out[8]=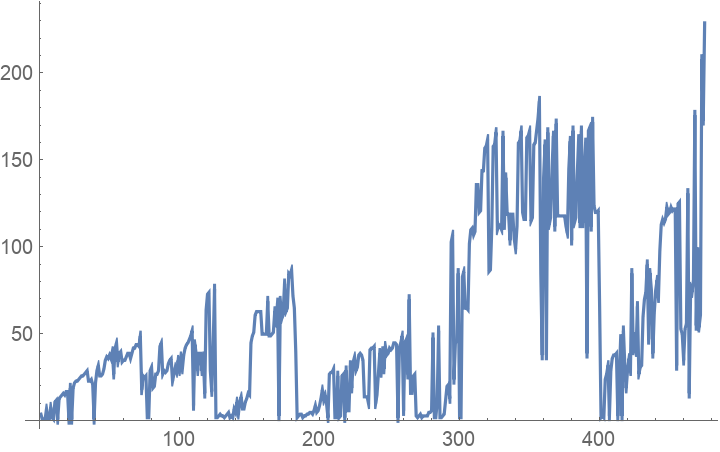

Create a key of axiom + theorem number:

In[9]:=
key = MapIndexed[# -> First[#2] &, SortBy[VertexList[ResourceData[\!\(\* TagBox["\"\<Theorem Network from Euclid's Elements\>\"", #& , BoxID -> "ResourceTag-Theorem Network from Euclid's Elements-Input", AutoDelete->True]\)]], Length]];

Make a map of what theorem references which others:

In[10]:=
ListPlot[List @@@ (EdgeList[ResourceData[\!\(\* TagBox["\"\<Theorem Network from Euclid's Elements\>\"", #& , BoxID -> "ResourceTag-Theorem Network from Euclid's Elements-Input", AutoDelete->True]\)]] /. key), AspectRatio -> 1]
Out[10]=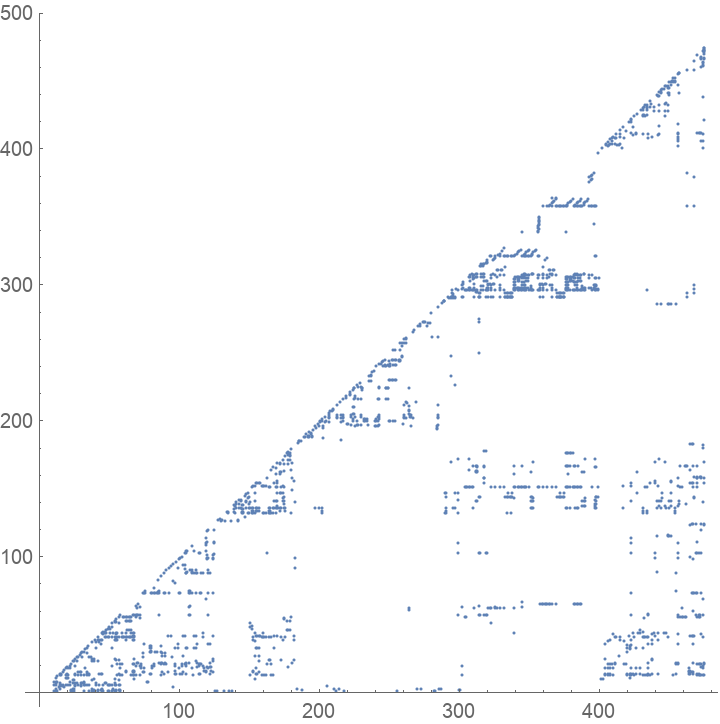

Wolfram Research, "Theorem Network from Euclid's Elements" from the Wolfram Data Repository (2020) https://doi.org/10.24097/wolfram.61787.data

Data Resource History

  • Date Created: 28 June 2017
  • Updated: 8 September 2020

Source Metadata

  • Title: A New Kind of Science
  • Creator: Stephen Wolfram
  • Publisher: Wolfram Media
  • Date: 2002
  • Language: English
  • Citation: Stephen Wolfram “A New Kind of Science” (2002)

Publisher Information

  • Contributed By: Stephen Wolfram
  • Publisher of Record: Wolfram Research