Wolfram Data Repository
Immediate Computable Access to Curated Contributed Data
Fractal dimensions of coastlines of all countries, dependencies, and territories
A country’s coastline has no well-defined length, as its length depends on the length of the ruler used to estimate it. A shorter ruler allows for more accuracy in measuring complex, irregular coastlines; thus, as the ruler length decreases, the coastline length becomes theoretically infinite. This is known as the “Coastline Paradox”, which can be attributed to the fractal-like property of coastlines. A coastline’s fractal dimension provides a quantitative index of complexity, measuring how fast the estimated coastline length increases with respect to a smaller and smaller scale at which it is measured. This dataset was created to calculate and compare the fractal dimensions of coastlines around the world. This dataset contains the fractal dimensions of coastlines of 249 countries, dependencies, and territories, generated using ResourceFunction[“CoastlineFractalDimension”]. If a country is landlocked, its fractal dimension is 0.
| In[1]:= |
| In[2]:= | ![Association[
Entity["Country", "Afghanistan"] :> 0, Entity["Country", "AlandIslands"] :> 1.263951375685873, Entity["Country", "Albania"] :> 1.0315072797280447`, Entity["Country", "Algeria"] :> 0.9562458932631597, Entity["Country", "AmericanSamoa"] :> 1.1374326920108941`, Entity["Country", "Andorra"] :> 0, Entity["Country", "Angola"] :> 0.9567118079003217, Entity["Country", "Anguilla"] :> 1.0878026295575531`, Entity["Country", "AntiguaBarbuda"] :> 1.1580245346349132`, Entity["Country", "Argentina"] :> 1.0690736850986617`, Entity["Country", "Armenia"] :> 1.024478319584278, Entity["Country", "Aruba"] :> 1.0533326136774463`, Entity["Country", "Australia"] :> 1.1373128103223118`, Entity["Country", "Austria"] :> 0, Entity["Country", "Azerbaijan"] :> 1.0327777576074983`, Entity["Country", "Bahamas"] :> 1.2444210832436922`, Entity["Country", "Bahrain"] :> 1.1032329046436544`, Entity["Country", "Bangladesh"] :> 1.1656592107601809`, Entity["Country", "Barbados"] :> 1.0462264718348089`, Entity["Country", "Belarus"] :> 0, Entity["Country", "Belgium"] :> 1.0673130988063024`, Entity["Country", "Belize"] :> 1.0190483002447273`, Entity["Country", "Benin"] :> 1.1355334282966196`, Entity["Country", "Bermuda"] :> 1.1611652054853019`, Entity["Country", "Bhutan"] :> 0, Entity["Country", "Bolivia"] :> 0, Entity["Country", "BonaireSintEustatiusAndSaba"] :> 1.0298895882901968`, Entity["Country", "BosniaHerzegovina"] :> 1.0394263490892532`, Entity["Country", "Botswana"] :> 0, Entity["Country", "BouvetIsland"] :> 0.9869671149706379, Entity["Country", "Brazil"] :> 1.0365986540088816`, Entity["Country", "BritishIndianOceanTerritory"] :> 1.173131538310979, Entity["Country", "BritishVirginIslands"] :> 1.1097352644983083`, Entity["Country", "Brunei"] :> 1.0138514042787474`, Entity["Country", "Bulgaria"] :> 1.085132372221726, Entity["Country", "BurkinaFaso"] :> 0, Entity["Country", "Burundi"] :> 0, Entity["Country", "Cambodia"] :> 1.0785966556138937`, Entity["Country", "Cameroon"] :> 1.1307218583424676`, Entity["Country", "Canada"] :> 1.1909699439987433`, Entity["Country", "CapeVerde"] :> 1.075564423295296, Entity["Country", "CaymanIslands"] :> 1.0581605272607544`, Entity["Country", "CentralAfricanRepublic"] :> 0, Entity["Country", "Chad"] :> 0, Entity["Country", "Chile"] :> 1.1716508189869872`, Entity["Country", "China"] :> 1.1699805185793342`, Entity["Country", "ChristmasIsland"] :> 1.0228779301587527`, Entity["Country", "CocosKeelingIslands"] :> 1.1374982521283803`, Entity["Country", "Colombia"] :> 1.000107231963018, Entity["Country", "Comoros"] :> 1.0250783164504185`, Entity["Country", "CookIslands"] :> 0, Entity["Country", "CostaRica"] :> 1.0954178850533385`, Entity["Country", "Croatia"] :> 1.1178239815706734`, Entity["Country", "Cuba"] :> 1.1436569280561055`, Entity["Country", "Curacao"] :> 1.1194480222607364`, Entity["Country", "Cyprus"] :> 1.0774909576792118`, Entity["Country", "CzechRepublic"] :> 0, Entity["Country", "DemocraticRepublicCongo"] :> 1.029157739689596, Entity["Country", "Denmark"] :> 1.1769959040713776`, Entity["Country", "Djibouti"] :> 1.0769484576094144`, Entity["Country", "Dominica"] :> 1.0681892743815693`, Entity["Country", "DominicanRepublic"] :> 1.0932339387934227`, Entity["Country", "EastTimor"] :> 1.0341256418074742`, Entity["Country", "Ecuador"] :> 1.1084211427360935`, Entity["Country", "Egypt"] :> 1.0246752781145663`, Entity["Country", "ElSalvador"] :> 1.092380247065358, Entity["Country", "EquatorialGuinea"] :> 1.0135282688865823`, Entity["Country", "Eritrea"] :> 1.0697513523903077`, Entity["Country", "Estonia"] :> 1.0917045022051617`, Entity["Country", "Ethiopia"] :> 0, Entity["Country", "FalklandIslands"] :> 1.3212611820940092`, Entity["Country", "FaroeIslands"] :> 1.069822420097738, Entity["Country", "Fiji"] :> 1.1562136595024455`, Entity["Country", "Finland"] :> 1.2389254270976244`, Entity["Country", "France"] :> 1.0807931107371311`, Entity["Country", "FrenchGuiana"] :> 1.074195508129456, Entity["Country", "FrenchPolynesia"] :> 1.0842167820862953`, Entity["Country", "FrenchSouthernAndAntarcticLands"] :> 1.2558465968148527`, Entity["Country", "Gabon"] :> 1.153395754105123, Entity["Country", "Gambia"] :> 1.238782076070549, Entity["Country", "GazaStrip"] :> 0.9923273826138151, Entity["Country", "Georgia"] :> 1.0149586112411622`, Entity["Country", "Germany"] :> 1.1108989533680622`, Entity["Country", "Ghana"] :> 0.99461248171619, Entity["Country", "Gibraltar"] :> 1.1230184463519768`, Entity["Country", "Greece"] :> 1.199491512335574, Entity["Country", "Greenland"] :> 1.3123346556987743`, Entity["Country", "Grenada"] :> 1.1379166460252463`, Entity["Country", "Guadeloupe"] :> 1.0900947865973827`, Entity["Country", "Guam"] :> 1.0735412321474762`, Entity["Country", "Guatemala"] :> 1.0480948806113342`, Entity["Country", "Guernsey"] :> 1.1414317964606646`, Entity["Country", "Guinea"] :> 1.2659535044420076`, Entity["Country", "GuineaBissau"] :> 1.4583778662990092`, Entity["Country", "Guyana"] :> 1.02022503009086, Entity["Country", "Haiti"] :> 1.0949560509676648`, Entity["Country", "Honduras"] :> 1.1178996904197829`, Entity["Country", "HongKong"] :> 1.202723048715046, Entity["Country", "Hungary"] :> 0, Entity["Country", "Iceland"] :> 1.2236641205273318`, Entity["Country", "India"] :> 1.0671518224137988`, Entity["Country", "Indonesia"] :> 1.07783030343393, Entity["Country", "Iran"] :> 1.0208505150147311`, Entity["Country", "Iraq"] :> 0.986527343723731, Entity["Country", "Ireland"] :> 1.2665171315661743`, Entity["Country", "IsleOfMan"] :> 1.072954522140247, Entity["Country", "Israel"] :> 1.0451038232973306`, Entity["Country", "Italy"] :> 1.0675224711220108`, Entity["Country", "IvoryCoast"] :> 0.9833663650927669, Entity["Country", "Jamaica"] :> 1.1017948108879776`, Entity["Country", "Japan"] :> 1.169777460840479, Entity["Country", "Jersey"] :> 1.1073341478678533`, Entity["Country", "Jordan"] :> 0.9460108080394292, Entity["Country", "Kazakhstan"] :> 1.0089331962173615`, Entity["Country", "Kenya"] :> 1.0722409615789843`, Entity["Country", "Kiribati"] :> 0, Entity["Country", "Kosovo"] :> 0,
Entity["Country", "Kuwait"] :> 1.0991264381921844`, Entity["Country", "Kyrgyzstan"] :> 0, Entity["Country", "Laos"] :> 0,
Entity["Country", "Latvia"] :> 1.0188123311837085`, Entity["Country", "Lebanon"] :> 1.0175171759115287`, Entity["Country", "Lesotho"] :> 1.0683574321452458`, Entity["Country", "Liberia"] :> 1.004776606269496, Entity["Country", "Libya"] :> 0.9623149914801509, Entity["Country", "Liechtenstein"] :> 0, Entity["Country", "Lithuania"] :> 1.0747351013899769`, Entity["Country", "Luxembourg"] :> 0, Entity["Country", "Macau"] :> 1.1184627587726057`, Entity["Country", "Macedonia"] :> 0, Entity["Country", "Madagascar"] :> 1.1134417272326222`, Entity["Country", "Malawi"] :> 0, Entity["Country", "Malaysia"] :> 1.0940014968636895`, Entity["Country", "Maldives"] :> 0, Entity["Country", "Mali"] :> 0, Entity["Country", "Malta"] :> 1.1359025122268447`, Entity["Country", "MarshallIslands"] :> 1.1356266342963854`, Entity["Country", "Martinique"] :> 1.1487185318635107`, Entity["Country", "Mauritania"] :> 0.9785824918119401, Entity["Country", "Mauritius"] :> 1.0738067909292643`, Entity["Country", "Mayotte"] :> 1.1335486663339778`, Entity["Country", "Mexico"] :> 1.119814121862947, Entity["Country", "Micronesia"] :> 1.0710469818828319`, Entity["Country", "Moldova"] :> 0, Entity["Country", "Monaco"] :> 1.1410943856714941`, Entity["Country", "Mongolia"] :> 0, Entity["Country", "Montenegro"] :> 1.1883412534730735`, Entity["Country", "Montserrat"] :> 1.0131200220411845`, Entity["Country", "Morocco"] :> 1.0229666022489208`, Entity["Country", "Mozambique"] :> 1.0512659775523208`, Entity["Country", "Myanmar"] :> 1.1067349085521856`, Entity["Country", "Namibia"] :> 0.9313680550076269, Entity["Country", "Nauru"] :> 1.0046957562210186`, Entity["Country", "Nepal"] :> 0, Entity["Country", "Netherlands"] :> 1.1103788187419226`, Entity["Country", "NewCaledonia"] :> 1.1744343101780192`, Entity["Country", "NewZealand"] :> 1.2089714384793935`, Entity["Country", "Nicaragua"] :> 1.0796039177955934`, Entity["Country", "Niger"] :> 0, Entity["Country", "Nigeria"] :> 1.182457516847974, Entity["Country", "Niue"] :> 1.0192589310312599`, Entity["Country", "NorfolkIsland"] :> 1.0522562544904333`, Entity["Country", "NorthernMarianaIslands"] :> 1.0448754529923603`, Entity["Country", "NorthKorea"] :> 1.1475154307180104`, Entity["Country", "Norway"] :> 1.372265748633463, Entity["Country", "Oman"] :> 0.9807054567283356, Entity["Country", "Pakistan"] :> 1.1075623729568747`, Entity["Country", "Palau"] :> 1.1436620368895327`, Entity["Country", "Panama"] :> 1.1504839066806731`, Entity["Country", "PapuaNewGuinea"] :> 1.1281513160093215`, Entity["Country", "Paraguay"] :> 0, Entity["Country", "Peru"] :> 1.0109240380914941`, Entity["Country", "Philippines"] :> 1.1756585352066513`, Entity["Country", "PitcairnIslands"] :> 0, Entity["Country", "Poland"] :> 1.0570514517461282`, Entity["Country", "Portugal"] :> 1.0884094223532117`, Entity["Country", "PuertoRico"] :> 1.1146004372308074`, Entity["Country", "Qatar"] :> 1.1265464287431628`, Entity["Country", "RepublicCongo"] :> 1.008350402852119, Entity["Country", "Reunion"] :> 1.0397648255463128`, Entity["Country", "Romania"] :> 1.0193667835531965`, Entity["Country", "Russia"] :> 1.147946914221042, Entity["Country", "Rwanda"] :> 0, Entity["Country", "SaintBarthelemy"] :> 1.1023109998477858`, Entity["Country", "SaintHelena"] :> 1.0914621904073984`, Entity["Country", "SaintKittsNevis"] :> 1.0539691260204798`, Entity["Country", "SaintLucia"] :> 1.1297394646017143`, Entity["Country", "SaintMartin"] :> 1.1044969849694908`, Entity["Country", "SaintPierreMiquelon"] :> 1.0691958424108494`, Entity["Country", "SaintVincentGrenadines"] :> 1.0597492657203507`, Entity["Country", "Samoa"] :> 1.1117568772524515`, Entity["Country", "SanMarino"] :> 1.0134276375923523`, Entity["Country", "SaoTomePrincipe"] :> 1.05992447796394, Entity["Country", "SaudiArabia"] :> 0.982956803421391, Entity["Country", "Senegal"] :> 1.124683251387241, Entity["Country", "Serbia"] :> 0, Entity["Country", "Seychelles"] :> 1.1243769255461873`, Entity["Country", "SierraLeone"] :> 1.1663781048161117`, Entity["Country", "Singapore"] :> 1.1477746179638224`, Entity["Country", "SintMaarten"] :> 1.0399581988471778`, Entity["Country", "Slovakia"] :> 0, Entity["Country", "Slovenia"] :> 1.02097239592567, Entity["Country", "SolomonIslands"] :> 1.1702793280254897`, Entity["Country", "Somalia"] :> 1.0010883407462994`, Entity["Country", "SouthAfrica"] :> 1.0354467322274084`, Entity["Country", "SouthGeorgiaAndTheSouthSandwichIslands"] :> 1.1656467687664473`, Entity["Country", "SouthKorea"] :> 1.230610995317527, Entity["Country", "SouthSudan"] :> 0, Entity["Country", "Spain"] :> 1.0762771245853027`, Entity["Country", "SriLanka"] :> 1.0834742130228028`, Entity["Country", "Sudan"] :> 1.0143778881268826`, Entity["Country", "Suriname"] :> 1.0315346320018828`, Entity["Country", "Svalbard"] :> 1.3184588282433627`, Entity["Country", "Swaziland"] :> 0, Entity["Country", "Sweden"] :> 1.2145719893997822`, Entity["Country", "Switzerland"] :> 0, Entity["Country", "Syria"] :> 0.9703320338345829, Entity["Country", "Taiwan"] :> 1.049195699589157, Entity["Country", "Tajikistan"] :> 0, Entity["Country", "Tanzania"] :> 1.0229822875120833`, Entity["Country", "Thailand"] :> 1.1166996588940945`, Entity["Country", "Togo"] :> 0, Entity["Country", "Tokelau"] :> 1.0849473828799556`, Entity["Country", "Tonga"] :> 1.1109252038693949`, Entity["Country", "TrinidadTobago"] :> 1.0773719489556883`, Entity["Country", "Tunisia"] :> 1.0845511068645461`, Entity["Country", "Turkey"] :> 1.1034791430734314`, Entity["Country", "Turkmenistan"] :> 1.109684400412446, Entity["Country", "TurksCaicosIslands"] :> 1.129497742280379, Entity["Country", "Tuvalu"] :> 1.1040691261342537`, Entity["Country", "Uganda"] :> 0, Entity["Country", "Ukraine"] :> 1.171061707523748, Entity["Country", "UnitedArabEmirates"] :> 1.1129240860340015`, Entity["Country", "UnitedKingdom"] :> 1.2154270232658364`, Entity["Country", "UnitedStates"] :> 1.0794141734131477`, Entity["Country", "UnitedStatesMinorOutlyingIslands"] :> 0, Entity["Country", "UnitedStatesVirginIslands"] :> 1.0918199150011207`, Entity["Country", "Uruguay"] :> 1.0163696724770974`, Entity["Country", "Uzbekistan"] :> 0, Entity["Country", "Vanuatu"] :> 1.051129161466665, Entity["Country", "VaticanCity"] :> 1.0199110383833854`, Entity["Country", "Venezuela"] :> 1.1450004032703347`, Entity["Country", "Vietnam"] :> 1.0492958691415506`, Entity["Country", "WallisFutuna"] :> 1.0324406544408262`, Entity["Country", "WestBank"] :> 1.0685687117796074`, Entity["Country", "WesternSahara"] :> 0.9706832184635219, Entity["Country", "Yemen"] :> 1.0228218291251656`, Entity["Country", "Zambia"] :> 0, Entity["Country", "Zimbabwe"] :> 0]](https://www.wolframcloud.com/obj/resourcesystem/images/8b7/8b7c6eec-c6c1-4393-90a2-5b14574ad288/7e625f5f7c3beece.png) |
Return the fractal dimension of the United Kingdom:
| In[3]:= |
| Out[3]= |
Get a Dataset ranking all countries, dependencies, and territories by their coastline fractal dimension:
| In[4]:= |
| In[5]:= |
| Out[5]= | 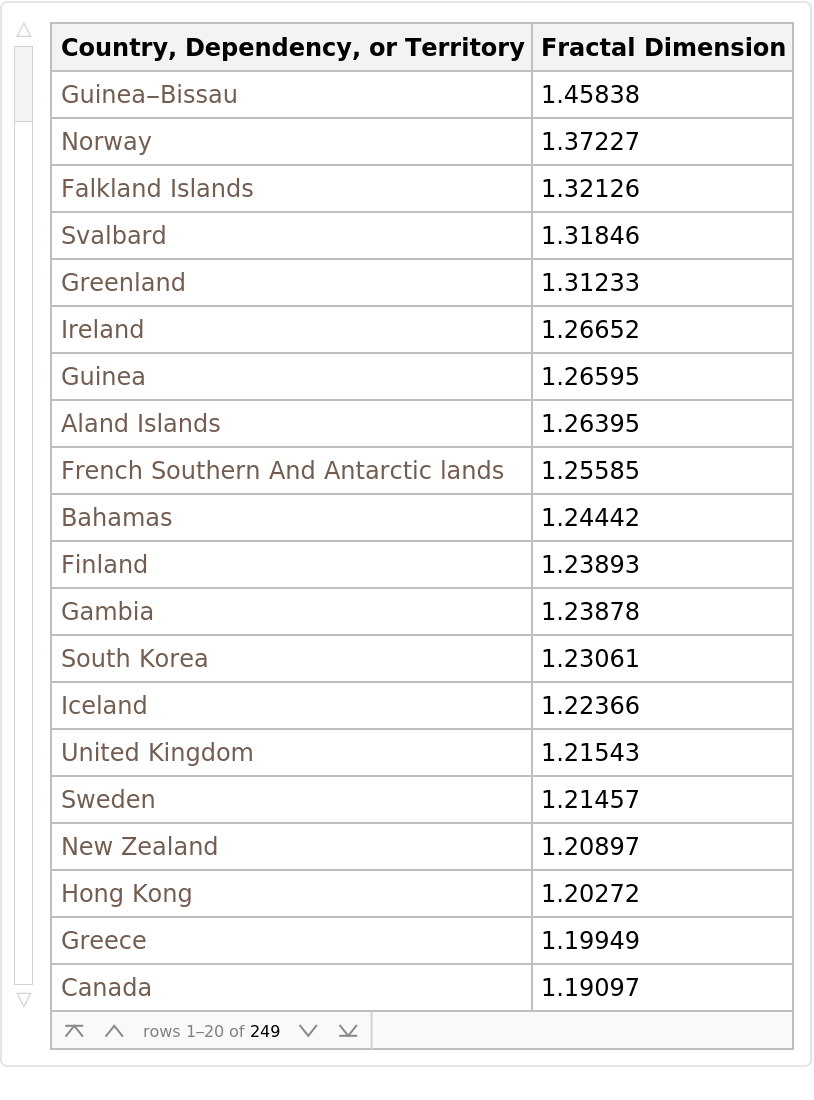 |
Generate a world map with each country, dependency, and territory labeled with a pop-up window with its fractal dimension:
| In[6]:= | ![DynamicGeoGraphics[
PopupWindow[GeoMarker[#, "Color" -> Purple], ResourceData["Coastline Fractal Dimensions"][#], WindowTitle -> #["Name"]] & /@ EntityList[EntityClass["Country", "Countries"]]]](https://www.wolframcloud.com/obj/resourcesystem/images/8b7/8b7c6eec-c6c1-4393-90a2-5b14574ad288/42e9cf8cde6c5b21.png) |
| Out[7]= | 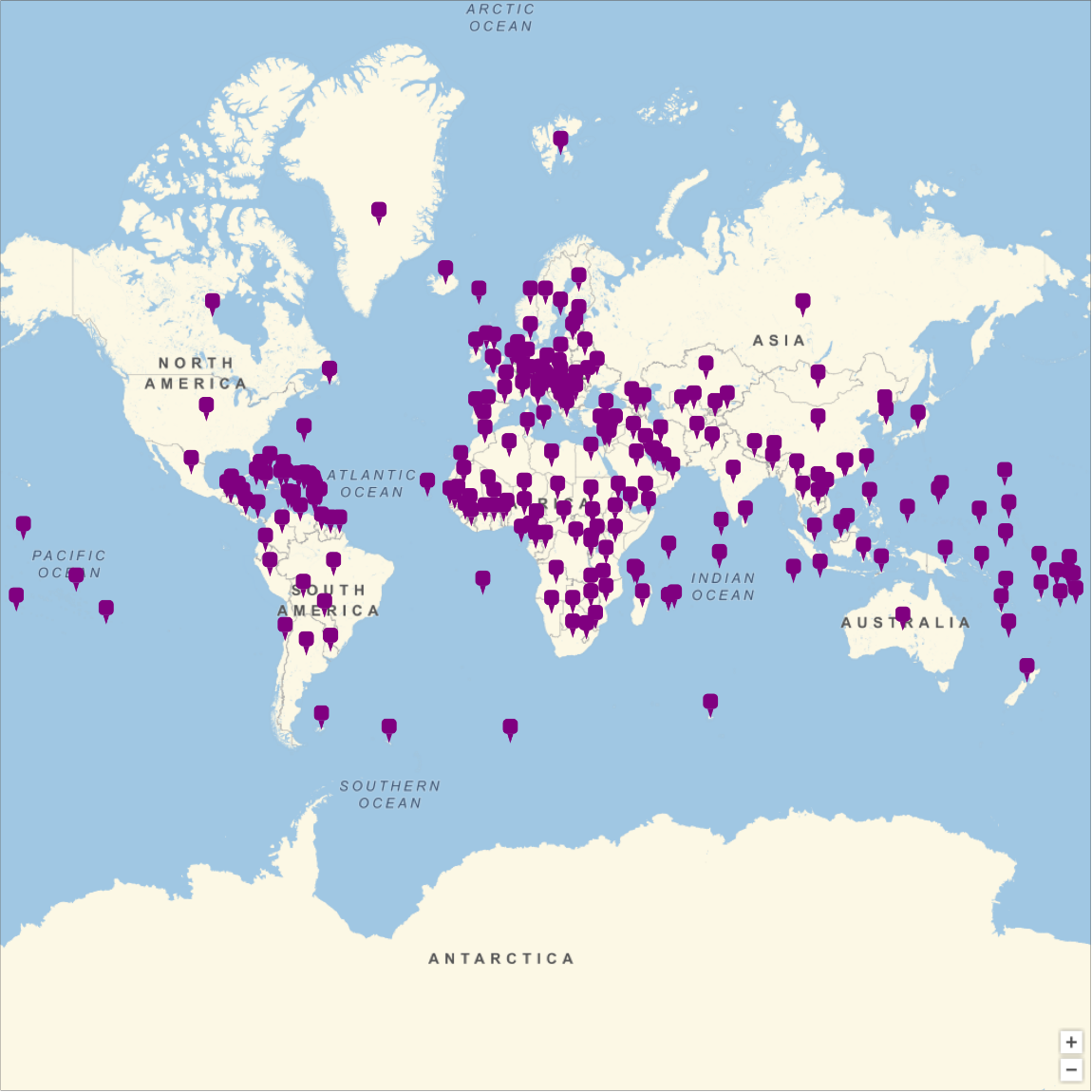 |
Compare coastline fractal dimensions around the world:
| In[8]:= |
| Out[8]= | 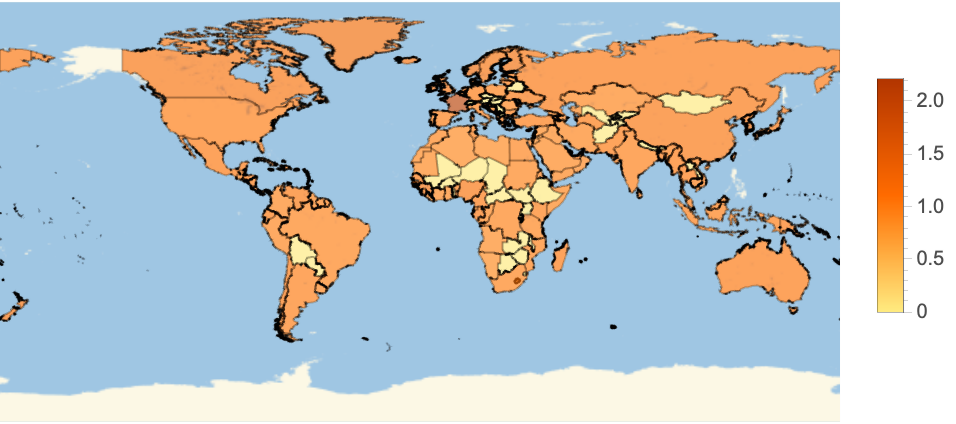 |
Generate a table to visualize the five countries, dependencies, and/or territories with the highest fractal dimensions:
| In[9]:= |
| In[10]:= | ![data = {#["Name"], Graphics[{FaceForm[], EdgeForm[Black], Polygon@Last[Sort[CountryData[#, "Shape"][[1, 3, 1]]]]}], sorted[EntityValue[#]]} & /@ Keys[sorted[[1 ;; 5]]];](https://www.wolframcloud.com/obj/resourcesystem/images/8b7/8b7c6eec-c6c1-4393-90a2-5b14574ad288/1fcaf007e5c79e2b.png) |
| In[11]:= | ![Text@Grid[
Prepend[ReverseSortBy[data, Last], {"Country Name", "Coastline", "Fractal Dimension"}], Background -> {None, {LightYellow, {White, Lighter[Blend[{Blue, Green}], .8]}}}, Frame -> All, ItemStyle -> {Automatic, Automatic, {{{1, 1}, {1, 3}} -> Bold}}]](https://www.wolframcloud.com/obj/resourcesystem/images/8b7/8b7c6eec-c6c1-4393-90a2-5b14574ad288/009da3a1c3bc2976.png) |
| Out[11]= |  |
Wolfram Summer Camp, "Coastline Fractal Dimensions" from the Wolfram Data Repository (2021)