Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Human Protein Protein Interaction Network

Source Notebook

The human protein protein interaction network from The Human Protein Atlas

Details

The data is based on The Human Protein Atlas version 23.0 and Ensembl version 109.
It is also possible to get the latest version (24.0) of the interaction data which was published on October 22, 2024.
The nodes of the graph are human protein coding genes involved in the protein protein interaction network (PPIN).
The default content is a Graph of the Human Protein Protein Interaction Network and these additional data:
"Version 24.0"Graph of all interacting genes in Version 24.0
"Human PPIN Graph measures"Graph related measures of the PPIN for Version 23.0

(11351 vertices, 63088 edges)

Examples

Basic Examples (1) 

The Human Protein Protein Interaction Network:

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Human Protein Protein Interaction Network\>\"", #& , BoxID -> "ResourceTag-Human Protein Protein Interaction Network-Input", AutoDelete->True]\)]
Out[1]=

Scope & Additional Elements (1) 

Data for Version 24.0 can be accessed using:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<Human Protein Protein Interaction Network\>\"", #& , BoxID -> "ResourceTag-Human Protein Protein Interaction Network-Input", AutoDelete->True]\), "Version 24.0"]
Out[2]=

Visualizations (3) 

Visualize the Human Protein Protein Interaction Network:

In[3]:=
humanPPIN = ResourceData[\!\(\* TagBox["\"\<Human Protein Protein Interaction Network\>\"", #& , BoxID -> "ResourceTag-Human Protein Protein Interaction Network-Input", AutoDelete->True]\)]; GraphPlot[humanPPIN, VertexStyle -> RGBColor[0.91, 0.68, 0], EdgeStyle -> RGBColor[0, 0.58, 0.61], VertexLabels -> Placed["Name", Tooltip]]
Out[4]=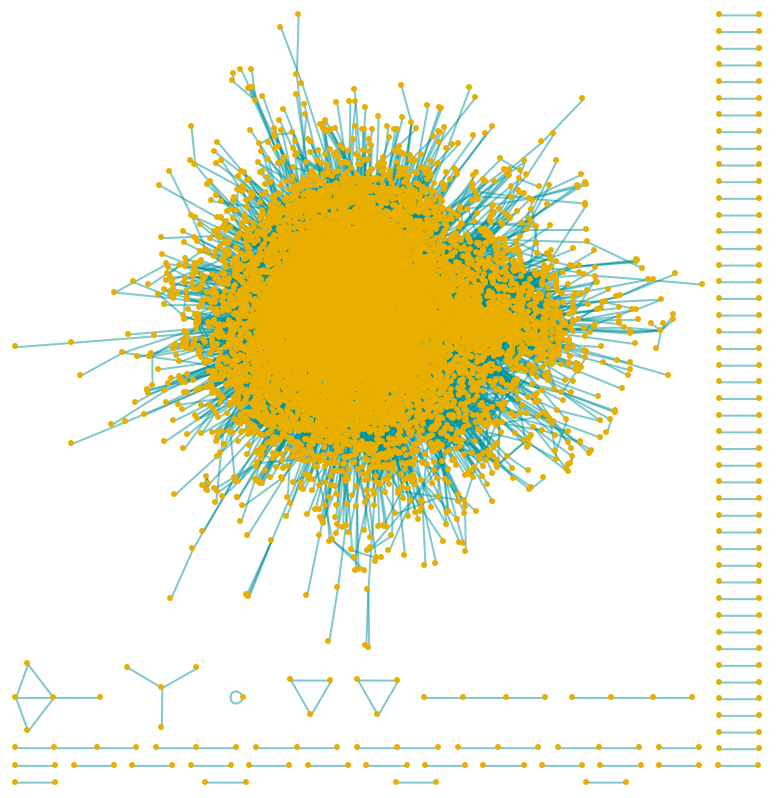

Let us visualize the power law distribution of VertexDegree in the Human PPIN, which implies the human PPIN is a scale-free network with a few large hubs:

In[5]:=
exponent = -2; fit = 5*(#^exponent) & /@ Range[300]; exponent2 = -1; fit2 = 0.3*(#^exponent2) & /@ Range[200]; ListLogLogPlot[{ResourceFunction[ ResourceObject[<|"Name" -> "VertexDegreeRelativeFrequencies", "ShortName" -> "VertexDegreeRelativeFrequencies", "UUID" -> "a76d6242-2a31-4326-bb6a-df4e446f50a6", "ResourceType" -> "Function", "Version" -> "1.0.0", "Description" -> "Relative frequencies of VertexDegree in a Graph", "RepositoryLocation" -> URL[ "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$8f984335e1b840a0b3c49438547b6dc4`VertexDegreeRelativeFrequencies", "FunctionLocation" -> CloudObject[ "https://www.wolframcloud.com/obj/beb446d6-a18b-4eae-b8fa-c7d76afd70c6"]|>, ResourceSystemBase -> Automatic]][humanPPIN], fit, fit2}, AxesLabel -> {"VertexDegree", "Probability"}, ImageSize -> 600, PlotLegends -> {"Data", "x^-2", "x^-1"}]
Out[6]=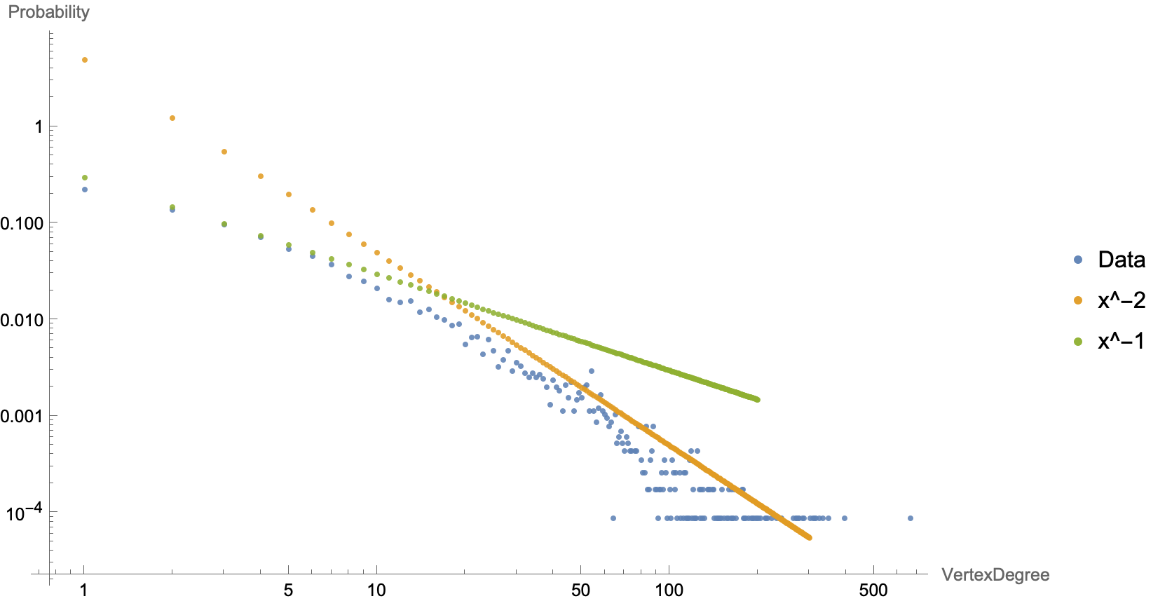

Which can be seen if the VertexSize of the nodes are scaled by its VertexDegree:

In[7]:=
ResourceFunction[ ResourceObject[<|"Name" -> "VertexSizeScaledGraph", "ShortName" -> "VertexSizeScaledGraph", "UUID" -> "82dfde6e-106f-4322-a329-1216e9f28362", "ResourceType" -> "Function", "Version" -> "1.1.0", "Description" -> "Visualize a graph with scaled vertex size based on custom graph related measures", "RepositoryLocation" -> URL[ "https://www.wolframcloud.com/obj/resourcesystem/api/1.0"], "SymbolName" -> "FunctionRepository`$4d8c3d76bc4e42be9489e98149696195`VertexSizeScaledGraph", "FunctionLocation" -> CloudObject[ "https://www.wolframcloud.com/obj/b0eb1e52-6cf3-4b6a-8efb-7950a9c63da5"]|>, ResourceSystemBase -> Automatic]][humanPPIN, VertexStyle -> RGBColor[0.91, 0.68, 0], EdgeStyle -> RGBColor[0, 0.58, 0.61], VertexLabels -> Placed["Name", Tooltip], "MaxVertexSize" -> 200]
Out[7]=

Analysis (5) 

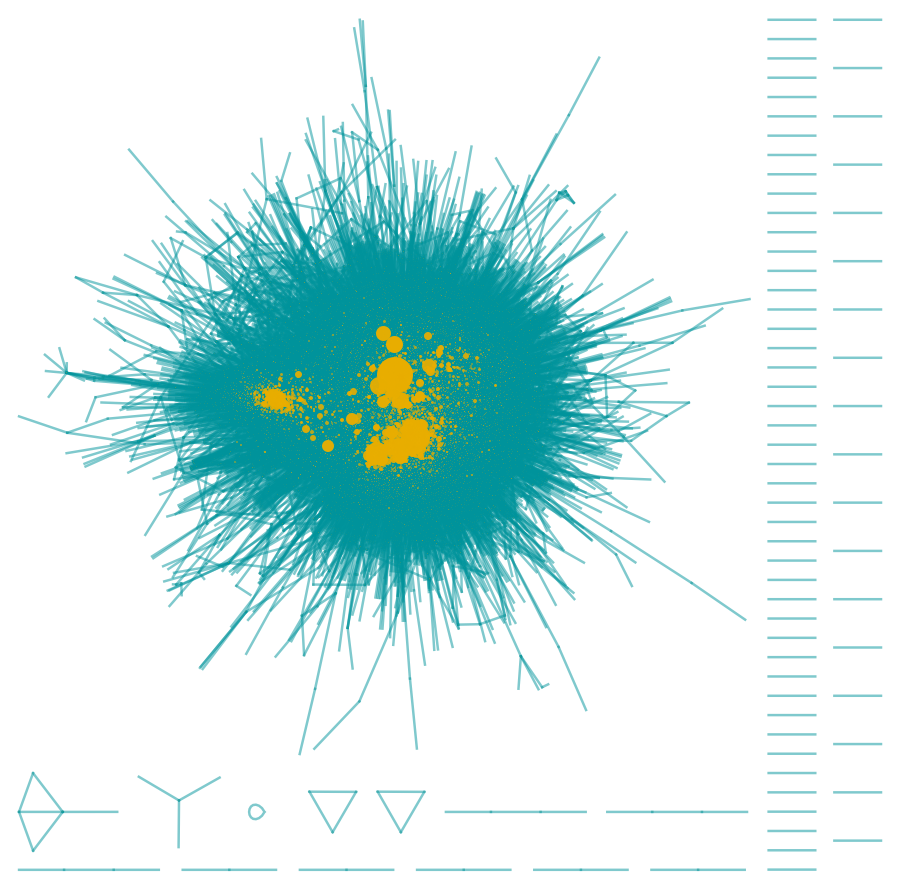A histogram displaying the distribution of degrees for the vertices of the graph, further confirming that the graph is a scale free network:

In[8]:=
humanPPIN = ResourceData[\!\(\* TagBox["\"\<Human Protein Protein Interaction Network\>\"", #& , BoxID -> "ResourceTag-Human Protein Protein Interaction Network-Input", AutoDelete->True]\)]; Histogram[VertexDegree[humanPPIN], PlotRange -> All, ScalingFunctions -> "Log", AxesLabel -> {"VertexDegree", "Frequency"}]
Out[9]=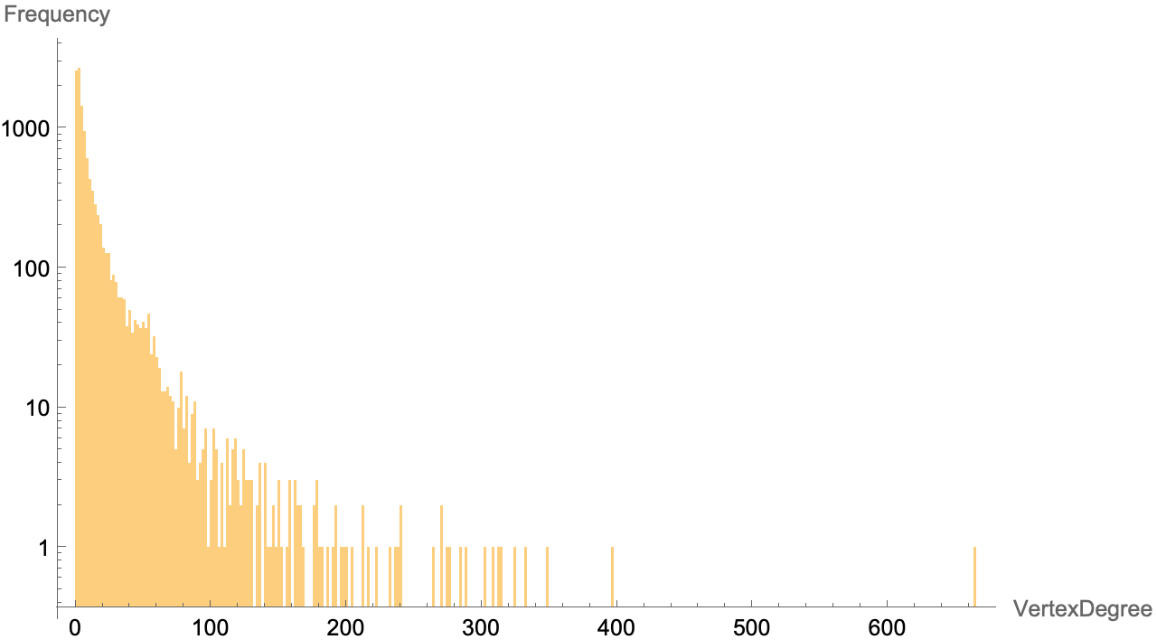

A table of the top 25 genes in the human body by degree, showing the behavior of "hubs" and how some genes interact with a large amount of genes:

In[10]:=
graphMeasures = ResourceData[\!\(\* TagBox["\"\<Human Protein Protein Interaction Network\>\"", #& , BoxID -> "ResourceTag-Human Protein Protein Interaction Network-Input", AutoDelete->True]\), "Human PPIN Graph measures"]; degreeRanking = ReverseSortBy[Map[#["DegreeCentrality"] &, graphMeasures], First -> Last]; Grid[Table[{Keys[degreeRanking][[i]], degreeRanking[[i]] }, {i, 25}], Frame -> All]
Out[11]=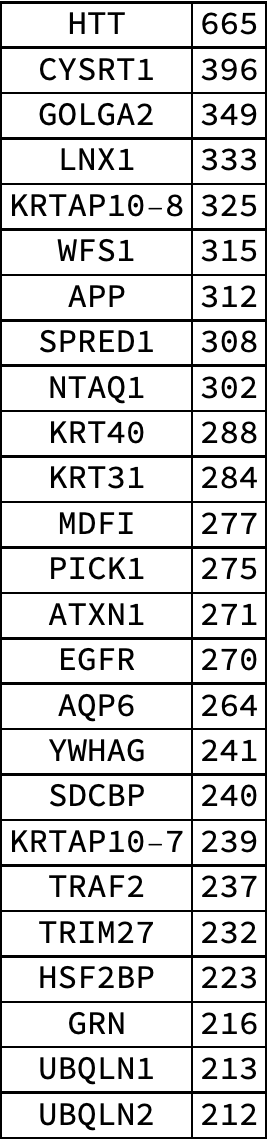

Visualizing the most important genes based on different centrality measures of the network:

In[12]:=
fontsize = 20; GraphicsRow[{WordCloud[Map[#["DegreeCentrality"] &, graphMeasures], PlotLabel -> Style["DegreeCentrality", Black, fontsize], ColorFunction -> "Rainbow", ImageSize -> 500], WordCloud[Map[#["BetweennessCentrality"] &, graphMeasures], PlotLabel -> Style["BetweennessCentrality", Black, fontsize], ColorFunction -> "Rainbow", ImageSize -> 500], WordCloud[Map[#["EigenvectorCentrality"] &, graphMeasures], PlotLabel -> Style["EigenvectorCentrality", Black, fontsize], ColorFunction -> "Rainbow", ImageSize -> 500]}, ImageSize -> 1000] // EchoTiming
18.157619`
Out[12]=

A dataset that contains the centrality measures for every single gene:

In[13]:=
graphMeasures = ResourceData[\!\(\* TagBox["\"\<Human Protein Protein Interaction Network\>\"", #& , BoxID -> "ResourceTag-Human Protein Protein Interaction Network-Input", AutoDelete->True]\), "Human PPIN Graph measures"]; Dataset@graphMeasures
Out[14]=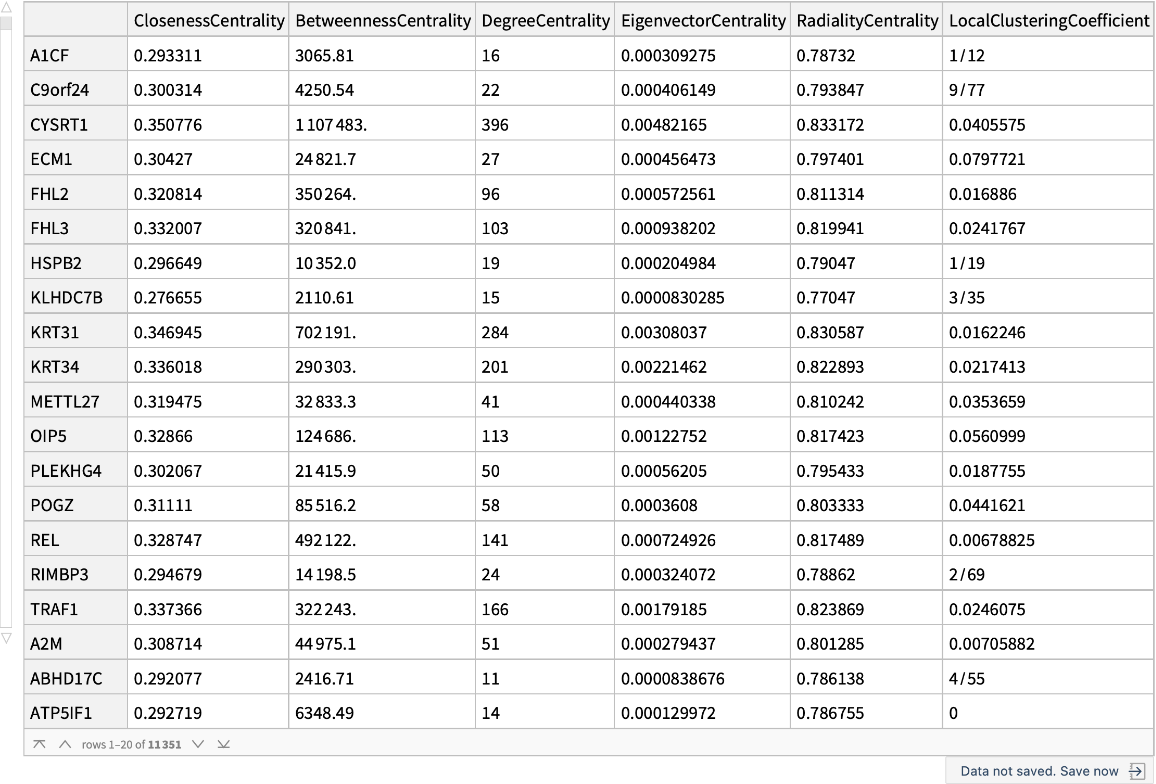

A dataset containing the top 1000 genes for each measure:

In[15]:=
measures = {"ClosenessCentrality", "BetweennessCentrality", "DegreeCentrality", "EigenvectorCentrality", "RadialityCentrality", "LocalClusteringCoefficient"}; geneOrdering = Table[ReverseSortBy[Map[#[k] &, graphMeasures], First -> Last], {k, measures}]; n = 1000; Dataset@ AssociationThread[ Table[i, {i, n}] -> MapThread[<|"ClosenessCentrality" -> #1, "BetweennessCentrality" -> #2, "DegreeCentrality" -> #3, "EigenvectorCentrality" -> #4, "RadialityCentrality" -> #5, "LocalClusteringCoefficient" -> #6|> &, ((Keys[#])[[ 1 ;; n]]) & /@ geneOrdering]]
Out[16]=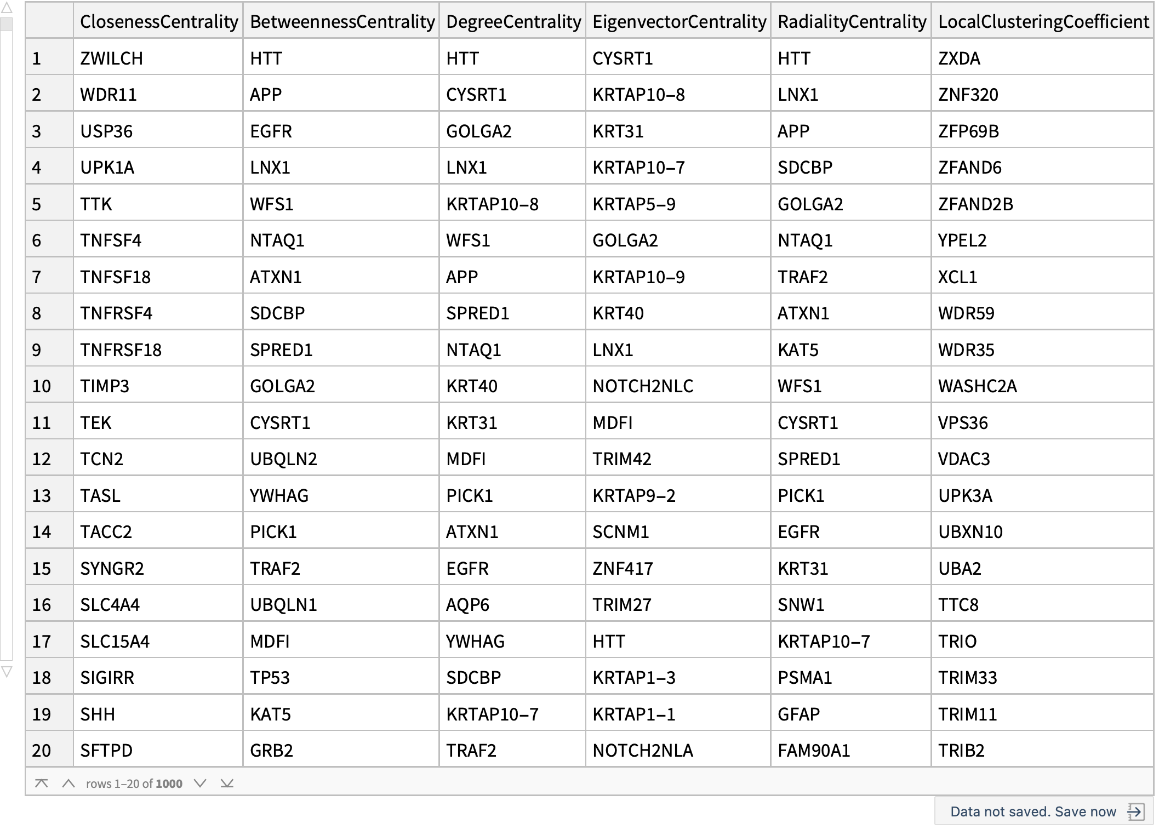

WolframChemistry, "Human Protein Protein Interaction Network" from the Wolfram Data Repository (2024)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • Uhlén M et al., Tissue-based map of the human proteome. Science (2015) PubMed: 25613900 DOI: 10.1126/science.1260419
    • Thul PJ et al., A subcellular map of the human proteome. Science. (2017) PubMed: 28495876 DOI: 10.1126/science.aal3321
    • Sjöstedt E et al., An atlas of the protein-coding genes in the human, pig, and mouse brain. Science. (2020) PubMed: 32139519 DOI: 10.1126/science.aay5947
    • Karlsson M et al., A single-cell type transcriptomics map of human tissues. Sci Adv. (2021) PubMed: 34321199 DOI: 10.1126/sciadv.abh2169
    • Uhlen M et al., A pathology atlas of the human cancer transcriptome. Science. (2017) PubMed: 28818916 DOI: 10.1126/science.aan2507
    • Uhlen M et al., A genome-wide transcriptomic analysis of protein-coding genes in human blood cells. Science. (2019) PubMed: 31857451 DOI: 10.1126/science.aax9198
    • Sjöstedt E et al., An atlas of the protein-coding genes in the human, pig, and mouse brain. Science. (2020) PubMed: 32139519 DOI: 10.1126/science.aay5947
    • Uhlén M et al., The human secretome. Sci Signal. (2019) PubMed: 31772123 DOI: 10.1126/scisignal.aaz0274
    • Becht, Etienne, et al. "Dimensionality reduction for visualizing single-cell data using UMAP." Nature biotechnology 37.1 (2019): 38-44.

See Also

Data Downloads

Publisher Information

  • Prepared for the Wolfram Data Repository By: David Wang
  • Publisher of Record: WolframChemistry