Wolfram Data Repository
Immediate Computable Access to Curated Contributed Data
Proportional-Derivative Op-amp Model
Model of a Proportional-Derivative (PD) controller op-amp circuit
Examples
Basic Examples (2)
Retrieve the model:
| In[1]:= | ![ResourceData[\!\(\*
TagBox["\"\<Proportional-Derivative Op-amp Model\>\"",
#& ,
BoxID -> "ResourceTag-Proportional-Derivative Op-amp Model-Input",
AutoDelete->True]\)]](https://www.wolframcloud.com/obj/resourcesystem/images/ba1/ba145076-0a3e-44d8-90af-ed31d97052ed/7aa4d164e68c552e.png){kind=small} |
| Out[1]= |  |
The icon:
| In[2]:= | ![ResourceData[\!\(\*
TagBox["\"\<Proportional-Derivative Op-amp Model\>\"",
#& ,
BoxID -> "ResourceTag-Proportional-Derivative Op-amp Model-Input",
AutoDelete->True]\), "Icon"]](https://www.wolframcloud.com/obj/resourcesystem/images/ba1/ba145076-0a3e-44d8-90af-ed31d97052ed/5e484875732c756f.png){kind=small} |
| Out[2]= |  |
Scope & Additional Elements (6)
Available content elements:
| In[3]:= | ![\!\(\*
TagBox[
RowBox[{"ResourceObject", "[", "\"\<Proportional-Derivative Op-amp Model\>\"", "]"}],
#& ,
BoxID -> "ResourceTag-Proportional-Derivative Op-amp Model-Input",
AutoDelete->True]\)["ContentElements"]](https://www.wolframcloud.com/obj/resourcesystem/images/ba1/ba145076-0a3e-44d8-90af-ed31d97052ed/4fe351d3bbf71eb3.png){kind=small} |
| Out[3]= |  |
The state space model:
| In[4]:= | ![ResourceData[\!\(\*
TagBox["\"\<Proportional-Derivative Op-amp Model\>\"",
#& ,
BoxID -> "ResourceTag-Proportional-Derivative Op-amp Model-Input",
AutoDelete->True]\), "StateSpaceModel"]](https://www.wolframcloud.com/obj/resourcesystem/images/ba1/ba145076-0a3e-44d8-90af-ed31d97052ed/141c9bca43629405.png){kind=small} |
| Out[4]= |  |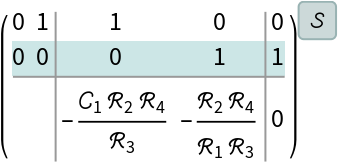
The input variables:
| In[5]:= | ![ResourceData[\!\(\*
TagBox["\"\<Proportional-Derivative Op-amp Model\>\"",
#& ,
BoxID -> "ResourceTag-Proportional-Derivative Op-amp Model-Input",
AutoDelete->True]\), "InputVariables"]](https://www.wolframcloud.com/obj/resourcesystem/images/ba1/ba145076-0a3e-44d8-90af-ed31d97052ed/73769be40554951d.png){kind=small} |
| Out[5]= |  |
The output variables:
| In[6]:= | ![ResourceData[\!\(\*
TagBox["\"\<Proportional-Derivative Op-amp Model\>\"",
#& ,
BoxID -> "ResourceTag-Proportional-Derivative Op-amp Model-Input",
AutoDelete->True]\), "OutputVariables"]](https://www.wolframcloud.com/obj/resourcesystem/images/ba1/ba145076-0a3e-44d8-90af-ed31d97052ed/642c5f5358063aa2.png){kind=small} |
| Out[6]= |  |
The complex variable:
| In[7]:= | ![ResourceData[\!\(\*
TagBox["\"\<Proportional-Derivative Op-amp Model\>\"",
#& ,
BoxID -> "ResourceTag-Proportional-Derivative Op-amp Model-Input",
AutoDelete->True]\), "ComplexVariable"]](https://www.wolframcloud.com/obj/resourcesystem/images/ba1/ba145076-0a3e-44d8-90af-ed31d97052ed/459362b10f271d90.png){kind=small} |
| Out[7]= |  |
The model parameters:
| In[8]:= | ![ResourceData[\!\(\*
TagBox["\"\<Proportional-Derivative Op-amp Model\>\"",
#& ,
BoxID -> "ResourceTag-Proportional-Derivative Op-amp Model-Input",
AutoDelete->True]\), "Parameters"]](https://www.wolframcloud.com/obj/resourcesystem/images/ba1/ba145076-0a3e-44d8-90af-ed31d97052ed/1685a51441139d06.png){kind=small} |
| Out[8]= |  |
Visualizations (1)
The proportional and derivative action for various input frequencies and component values:| In[9]:= | ![Manipulate[
Plot[{Sin[\[Omega] t], Evaluate[OutputResponse[ResourceData[\!\(\*
TagBox["\"\<Proportional-Derivative Op-amp Model\>\"",
#& ,
BoxID -> "ResourceTag-Proportional-Derivative Op-amp Model-Input",
AutoDelete->True]\)] /. {Subscript[\[ScriptCapitalR], 1] -> r1, Subscript[\[ScriptCapitalR], 2] -> r2, Subscript[\[ScriptCapitalR], 3] -> r3, Subscript[\[ScriptCapitalR], 4] -> r4, Subscript[\[ScriptCapitalC], 1] -> c1}, Sin[\[Omega] t], {t, 0, 10}]]}, {t, 0, 10}, Sequence[
PlotLegends -> Placed[{"input", "output"}, Below], Frame -> True]], Sequence[{{\[Omega], 1}, 0.1, 10, ImageSize -> 75},
Delimiter, {{r1, 100,
Subscript[\[ScriptCapitalR], 1]}, {100, 330, 500, 1000}}, {{r2, 330,
Subscript[\[ScriptCapitalR], 2]}, {100, 330, 500, 1000}}, {{r3, 330,
Subscript[\[ScriptCapitalR], 3]}, {100, 330, 500, 1000}}, {{r4, 330,
Subscript[\[ScriptCapitalR], 4]}, {100, 330, 500, 1000}}, {{c1, 0.01,
Subscript[\[ScriptCapitalC], 1]}, {0.005, 0.01, 0.025, 0.1}}], Sequence[ControlPlacement -> Left, SaveDefinitions -> True]
]](https://www.wolframcloud.com/obj/resourcesystem/images/ba1/ba145076-0a3e-44d8-90af-ed31d97052ed/560d9737e3f1c857.png) |
| Out[9]= |  |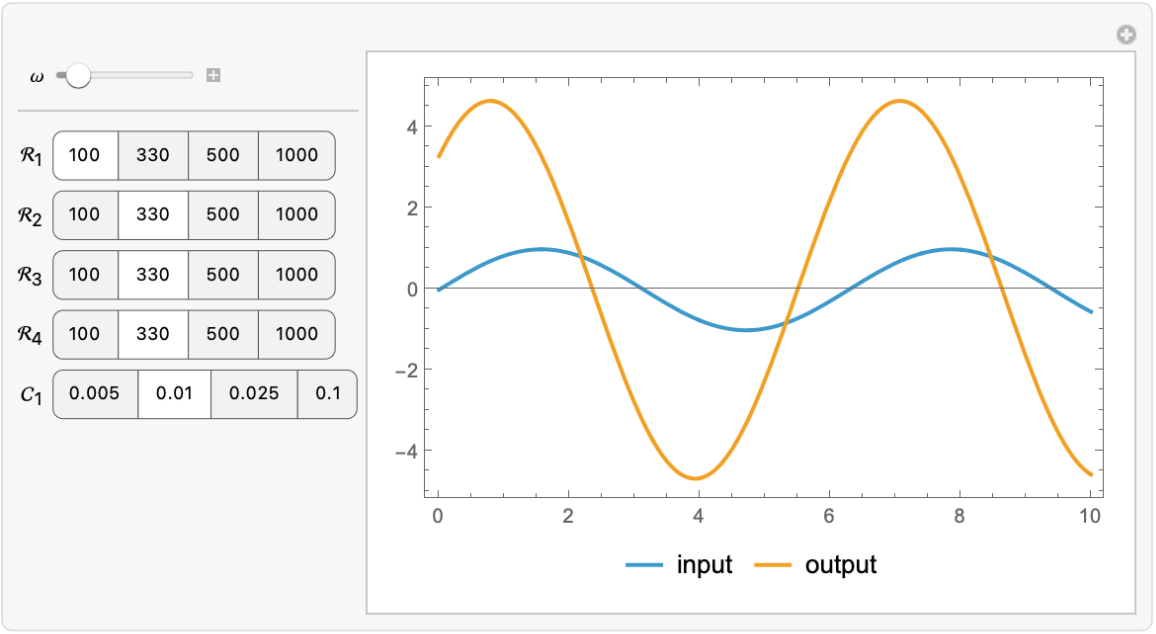
Analysis (1)
The magnitude increases 20dB every decade above the cutoff frequency, and phase starts from 0 and reaches 90 °:| In[10]:= | ![Manipulate[BodePlot[ResourceData[\!\(\*
TagBox["\"\<Proportional-Derivative Op-amp Model\>\"",
#& ,
BoxID -> "ResourceTag-Proportional-Derivative Op-amp Model-Input",
AutoDelete->True]\)] /. {Subscript[\[ScriptCapitalR], 1] -> r1, Subscript[\[ScriptCapitalR], 2] -> r2, Subscript[\[ScriptCapitalR], 3] -> r3, Subscript[\[ScriptCapitalR], 4] -> r4, Subscript[\[ScriptCapitalC], 1] -> c1}, Sequence[
GridLines -> {{{c1^(-1)/r1}, None}, {{c1^(-1)/r1}, {45}}}, PlotRange -> {Automatic, {0, 91}}, ImageSize -> Small, PlotLayout -> "HorizontalGrid", PlotLabel -> {"magnitude", "phase"}]], Grid[{{
Control[{{r1, 100,
Subscript[\[ScriptCapitalR], 1]}, {100, 330, 500, 1000}}],
Control[{{r3, 330,
Subscript[\[ScriptCapitalR], 3]}, {100, 330, 500, 1000}}],
Control[{{c1, 0.01,
Subscript[\[ScriptCapitalC], 1]}, {0.005, 0.01, 0.025, 0.1}}]}, {
Control[{{r2, 330,
Subscript[\[ScriptCapitalR], 2]}, {100, 330, 500, 1000}}],
Control[{{r4, 330,
Subscript[\[ScriptCapitalR], 4]}, {100, 330, 500, 1000}}], Null}}, Spacings -> 2], SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/ba1/ba145076-0a3e-44d8-90af-ed31d97052ed/75d2e0477ca255c5.png) |
| Out[10]= |  |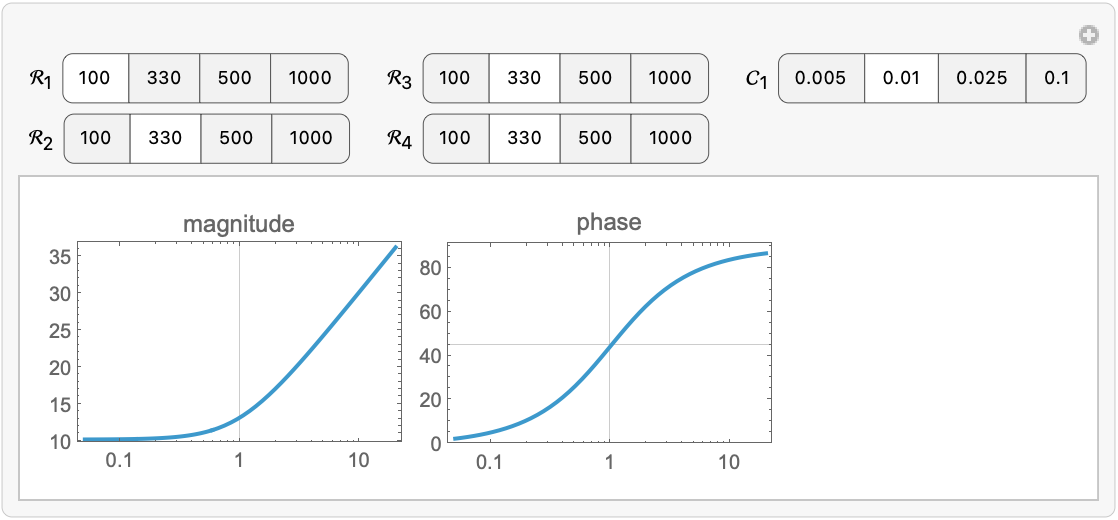
Bibliographic Citation
Suba Thomas, "Proportional-Derivative Op-amp Model" from the Wolfram Data Repository (2025)