Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

Inverted Pendulum Model

Source Notebook

A model of an inverted pendulum on a cart

Examples

Basic Examples (3) 

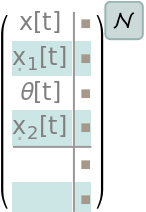
Retrieve the model:

In[1]:=
ResourceData[\!\(\* TagBox["\"\<Inverted Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Inverted Pendulum Model-Input", AutoDelete->True]\)]
Out[1]=

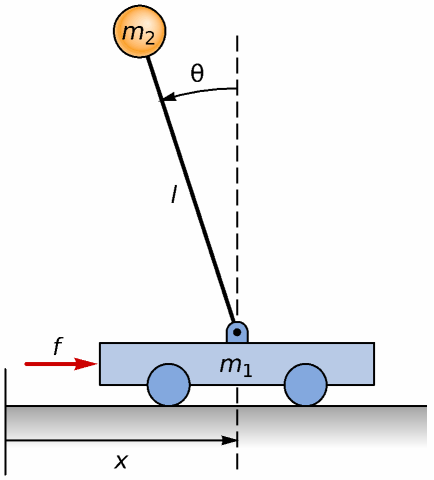
The icon:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<Inverted Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Inverted Pendulum Model-Input", AutoDelete->True]\), "Icon"]
Out[2]=

The annotation:

In[3]:=
ResourceData[\!\(\* TagBox["\"\<Inverted Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Inverted Pendulum Model-Input", AutoDelete->True]\), "Annotation"]
Out[3]=

Scope & Additional Elements (4) 

Available content elements:

In[4]:=
\!\(\* TagBox[ RowBox[{"ResourceObject", "[", "\"\<Inverted Pendulum Model\>\"", "]"}], #& , BoxID -> "ResourceTag-Inverted Pendulum Model-Input", AutoDelete->True]\)["ContentElements"]
Out[4]=

The available model types:

In[5]:=
ResourceData[\!\(\* TagBox["\"\<Inverted Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Inverted Pendulum Model-Input", AutoDelete->True]\), "AvailableModelTypes"]
Out[5]=

The operating point:

In[6]:=
ResourceData[\!\(\* TagBox["\"\<Inverted Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Inverted Pendulum Model-Input", AutoDelete->True]\), "OperatingPoint"]
Out[6]=

The parameters:

In[7]:=
ResourceData[\!\(\* TagBox["\"\<Inverted Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Inverted Pendulum Model-Input", AutoDelete->True]\), "Parameters"]
Out[7]=

Visualizations (2) 

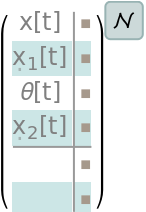
The numerical model of the system:

In[8]:=
nssm = ResourceData[\!\(\* TagBox["\"\<Inverted Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Inverted Pendulum Model-Input", AutoDelete->True]\), "NonlinearStateSpaceModel"] /. ResourceData[\!\(\* TagBox["\"\<Inverted Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Inverted Pendulum Model-Input", AutoDelete->True]\), "Parameters"]
Out[8]=

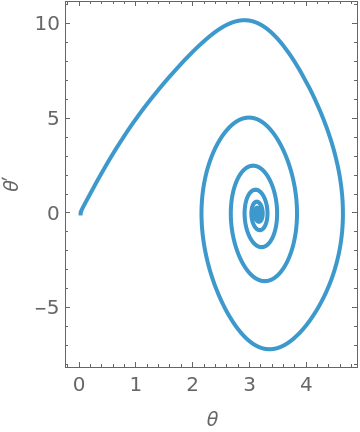
A parametric plot of the pendulum's angular position and velocity:

In[9]:=
sr = StateResponse[{nssm, {0, 0, 1 °, 0}}, 0, {t, 0, 10}];
In[10]:=
ParametricPlot[sr[[3 ;; 4]], {t, 0, 10}, Sequence[ PlotRange -> All, AspectRatio -> Full, ImageSize -> Small, Frame -> True, Axes -> False, FrameLabel -> {\[Theta], Derivative[1][\[Theta]]}]]
Out[10]=

Analysis (3) 

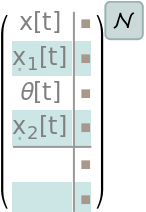
The numerical model:

In[11]:=
ResourceData[\!\(\* TagBox["\"\<Inverted Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Inverted Pendulum Model-Input", AutoDelete->True]\), "NonlinearStateSpaceModel"] /. ResourceData[\!\(\* TagBox["\"\<Inverted Pendulum Model\>\"", #& , BoxID -> "ResourceTag-Inverted Pendulum Model-Input", AutoDelete->True]\), "Parameters"]
Out[11]=

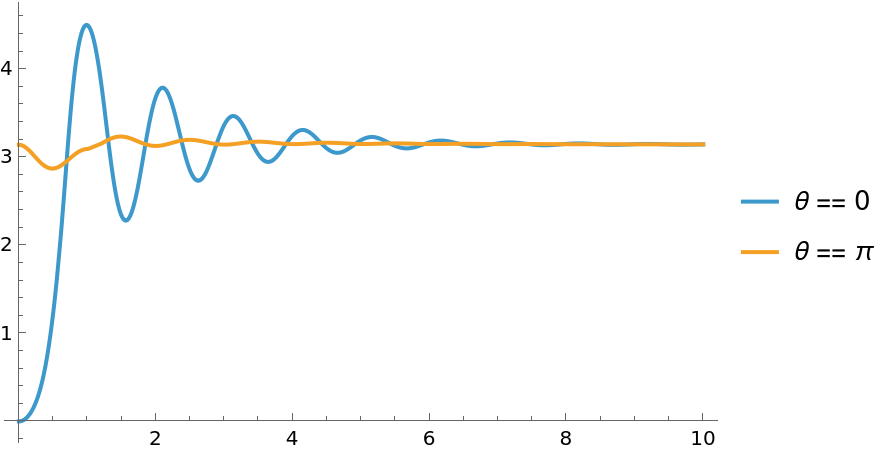
Responses starting from the upright and downright positions:

In[12]:=
Table[OutputResponse[{%, {0, 0, \[Theta]0, 0}}, UnitBox[t - 0.5], {t, 0, 10}][[2]], {\[Theta]0, {0, \[Pi]}}]
Out[12]=

Both responses settle in the stable downward position:

In[13]:=
Plot[%, {t, 0, 10}, PlotRange -> All, PlotLegends -> {"\[Theta] == 0", "\[Theta] == \[Pi]"}]
Out[13]=

Suba Thomas, "Inverted Pendulum Model" from the Wolfram Data Repository (2025)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • K. J. Åström and R. M. Murray, "Feedback Systems: An Introduction for Scientists and Engineers", Princeton Univ. Press, 2008.

Publisher Information

  • Prepared for the Wolfram Data Repository By: Maher Kuzbari, Suba Thomas
  • Publisher of Record: Suba Thomas