Wolfram Data Repository

Immediate Computable Access to Curated Contributed Data

747 Longitudinal Model

Source Notebook

Model of the longitudinal dynamics of a Boeing 747

Examples

Basic Examples (3) 

Retrieve the model:

In[1]:=
ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\)]
Out[1]=

The icon:

In[2]:=
ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\), "Icon"]
Out[2]=

The annotation:

In[3]:=
ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\), "Annotation"]
Out[3]=

Scope & Additional Elements (5) 

Available content elements:

In[4]:=
\!\(\* TagBox[ RowBox[{"ResourceObject", "[", "\"\<747 Longitudinal Model\>\"", "]"}], #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\)["ContentElements"]
Out[4]=

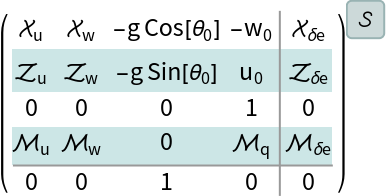
The transfer function model:

In[5]:=
ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\), "TransferFunctionModel"]
Out[5]=

The input variables:

In[6]:=
ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\), "InputVariables"]
Out[6]=

Other variables:

In[7]:=
ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\), "OtherVariables"]
Out[7]=

Temporal variable:

In[8]:=
ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\), "TemporalVariable"]
Out[8]=

Visualizations (1) 

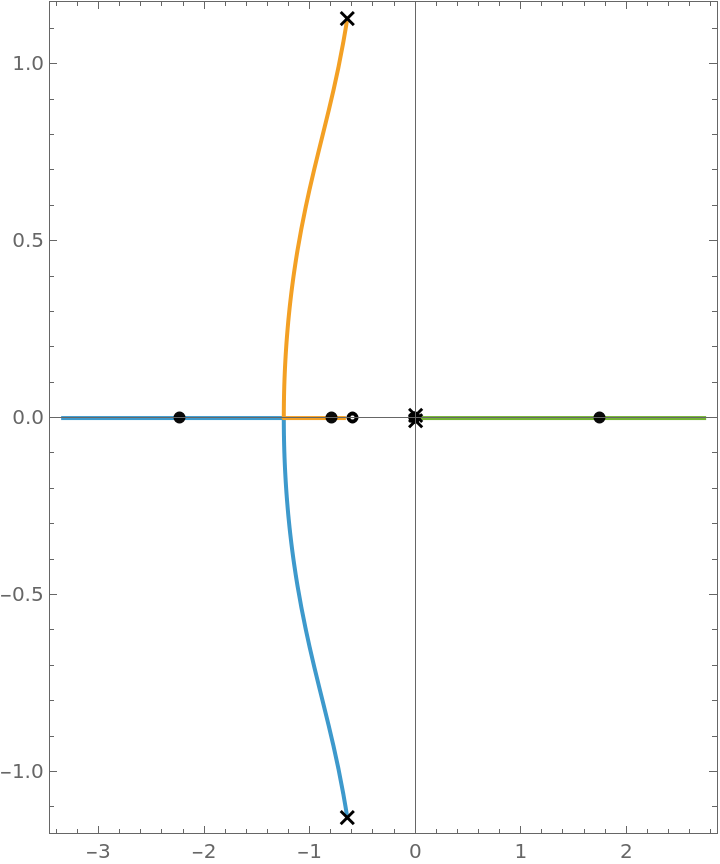
A root-locus plot of the system:

In[9]:=
RootLocusPlot[k (ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\), "TransferFunctionModel"] /. ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\), "Parameters"])[s], {k, 0, 5}, AspectRatio -> Full, Frame -> True, PlotRange -> All]
Out[9]=

Analysis (2) 

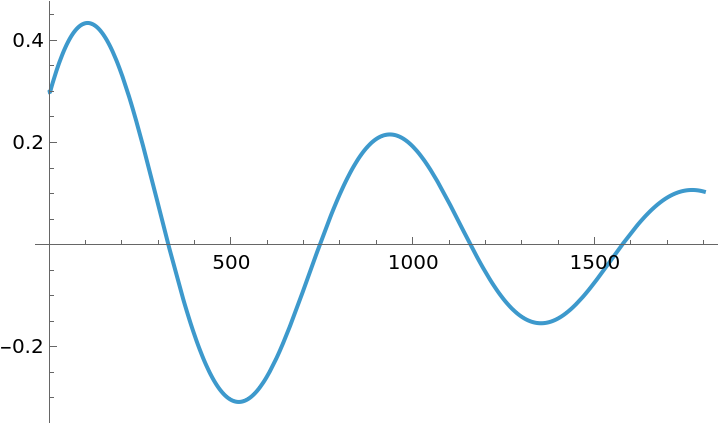
Its response to an initial perturbation in the pitch angle θ is sluggish and oscillatory:
In[10]:=
OutputResponse[{ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\)] /. ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\), "Parameters"], {0, 0, 0.3}}, 0, {t, 0, 1800}]; Plot[%, {t, 0, 1800}, PlotRange -> All]
Out[11]=
This is because the eigenvalues of the linear system are close to the imaginary axis:
In[12]:=
MatrixForm[Eigenvalues[Normal[ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\), "StateSpaceModel"]][[1]] /. ResourceData[\!\(\* TagBox["\"\<747 Longitudinal Model\>\"", #& , BoxID -> "ResourceTag-747 Longitudinal Model-Input", AutoDelete->True]\), "Parameters"]]]
Out[12]=

Suba Thomas, "747 Longitudinal Model" from the Wolfram Data Repository (2025)  

Data Resource History

  • Date Created:

Source Metadata

  • Citation:
    • G. F. Franklin, J. D. Powell, and A. Emami-Naeini, "Feedback Control of Dynamic Systems", 8th ed. Boston, MA, USA: Pearson, 2019, p. 1712.

Publisher Information

  • Prepared for the Wolfram Data Repository By: Maher Kuzbari, Suba Thomas
  • Publisher of Record: Suba Thomas